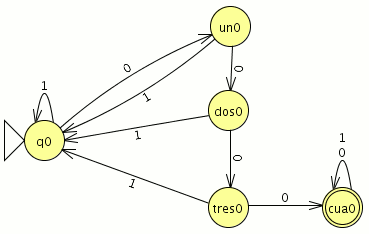
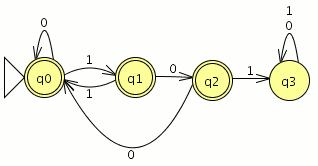
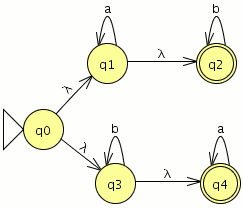
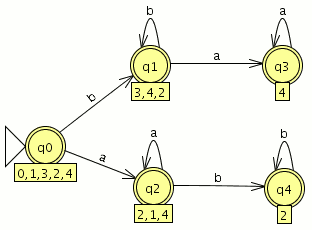
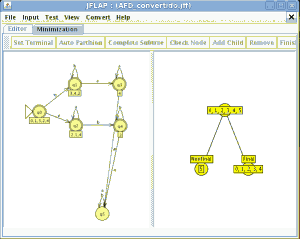
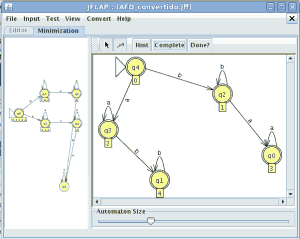
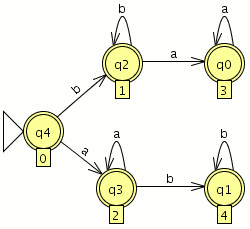
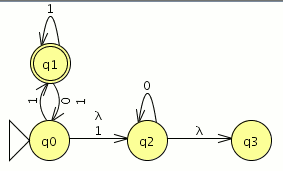
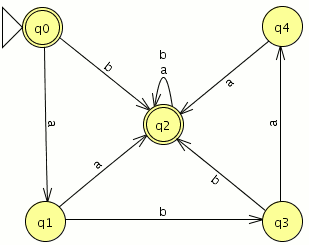
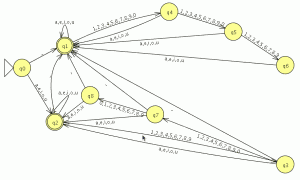
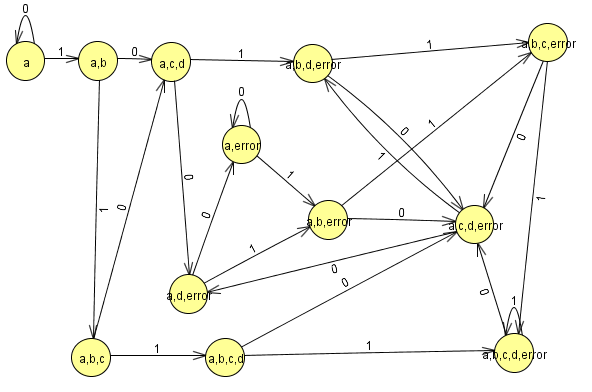
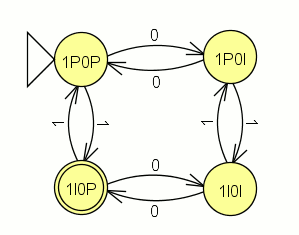
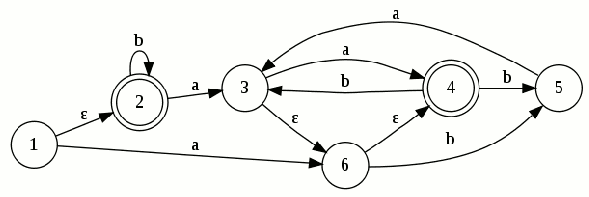
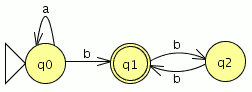P1: Convierte el siguiente AFND–ε en un AFND (incluye todas las tablas, grafos, quintuplas, y el cálculo de la clausura transitiva necesario). El estado inicial es el estado 1.
Hagamos memoria una quintupla se representa por esta formula 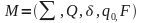 donde:
donde:
 es un alfabeto
es un alfabeto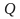 es un conjunto finito no vació de estados
es un conjunto finito no vació de estados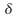 es una función de transición
es una función de transición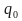 es el estado inicial
es el estado inicial- F es el conjunto de estados finales
Para el AFND–ε la quintupla estará formada por:
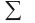 ={a,b,ε}
={a,b,ε}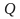 ={1,2,3,4,5,6}
={1,2,3,4,5,6}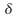 la tabla de transición
la tabla de transición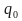 ={1}
={1}- F={2,4}
Creamos la tabla de transición para el AFND-ε
| Elemento |
a |
b |
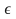
|
|
1
|
{6} |
{ } } |
{2} |
|
2
|
{3} |
{2} |
{ } } |
|
3
|
{4} |
{ } } |
{6} |
|
4
|
{ } } |
{3,5} |
{ } } |
|
5
|
{3} |
{ } } |
{ } } |
|
6
|
{ } } |
{5} |
{4} |
ahora calculamos las clausuras para cada elemento
Por clausura de un elemento entendemos el conjunto de estados a los que podemos acceder sin consumir ninguna símbolo , el propio elemento al que le calculamos su clausura pertenecerá a la misma.
para que quede mas claro, para el elemento 3 su clausuara estara compuesta por 3, 6 “(3,ε)=6” y 4 “(6,ε)=4”
| Elemento |
a |
b |
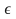 |
clausura |
| 1 |
{6} |
{ } } |
{2} |
{1,2} = Cl(1) |
| 2 |
{3} |
{2} |
{ } } |
{2} = Cl(2) |
| 3 |
{4} |
{ } } |
{6} |
{3,6,4} = Cl(3) |
| 4 |
{ } } |
{3,5} |
{ } } |
{4} = Cl(4) |
| 5 |
{3} |
{ } } |
{ } } |
{5} = Cl(5) |
| 6 |
{ } } |
{5} |
{4} |
{6,4} = Cl(6) |
Ahora creamos una nueva tabla eliminando la columna de ε y substituyendo los estados de destino para cada elemento del alfabeto por la unión de los estados de destino de la clausura. Por ejemplo para el elemento 1 la clausura es {1,2} y para la transición con a debemos incluir 6 para el estado 1 y 3 para el estado 2. por lo tanto nos queda el conjunto {6,3}.
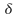 |
a |
b |
| Cl(1) |
{6,3}
|
{2}
|
| Cl(2) |
{3}
|
{2}
|
| Cl(3) |
{4}
|
{3,5} |
| Cl(4) |
{ } } |
{3,5} |
| Cl(5) |
{3}
|
{ } } |
| Cl(6) |
{ } } |
{3,5} |
una vez realizada esta tabla creamos la ultima tabla substituyendo cada estado destino de la tabla anterior por la clausura del mismo
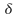 |
a |
b |
| Cl(1) |
{3,4,6}
|
{2}
|
| Cl(2) |
{3,4,6}
|
{2}
|
| Cl(3) |
{4}
|
{3,4,5,6}
|
| Cl(4) |
{ } }
|
{3,4,5,6}
|
| Cl(5) |
{3,4,6}
|
{ } }
|
| Cl(6) |
{ } }
|
{3,4,5,6}
|
Ahora ajustamos los estados para añadir los iniciales y los finales. Si en la clausura de un elemento existe un estado inicial este es inicial (marcados verde en la segunda tabla) y si existe un estado final este es final (marcados de rojo en la segunda tabla) con esto ya tenemos el AFND sin transiciones epsilon
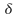 |
a |
b |
| *->Cl(1) |
{3,4,6}
|
{2}
|
| *Cl(2) |
{3,4,6}
|
{2}
|
| *Cl(3) |
{4}
|
{3,4,5,6}
|
| *Cl(4) |
{ } }
|
{3,4,5,6}
|
| Cl(5) |
{3,4,6}
|
{ } }
|
| *Cl(6) |
{ } }
|
{3,4,5,6}
|
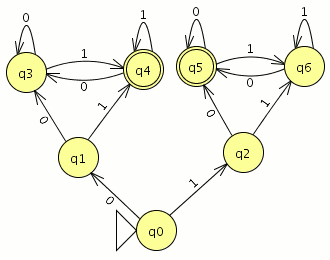
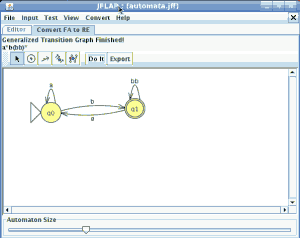
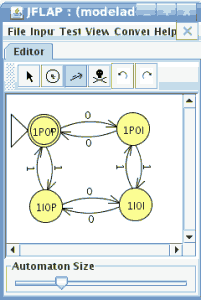
Para el AFND la quintupla estará formada por:
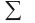 ={a,b}
={a,b}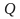 ={1,2,3,4,5,6}
={1,2,3,4,5,6}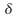 la tabla de transición
la tabla de transición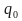 ={1}
={1}- F={1,2,3,4,6}
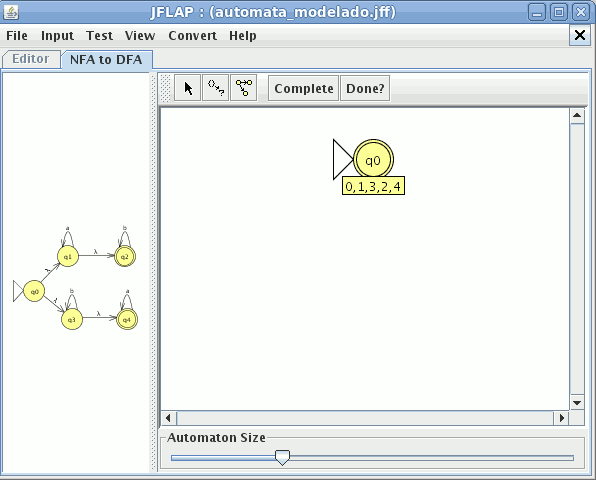
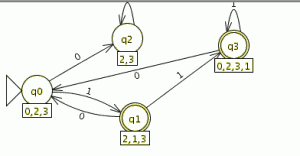
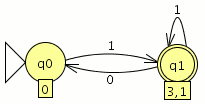
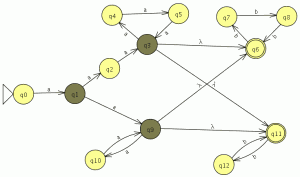
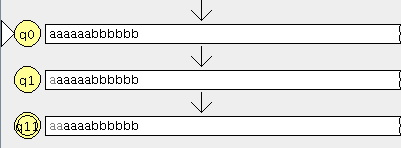
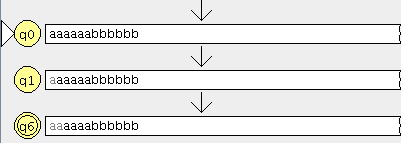
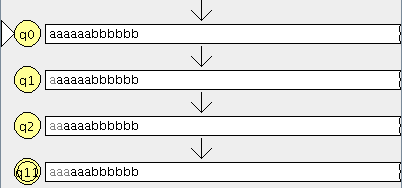
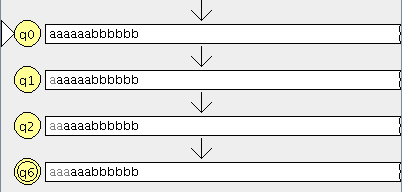
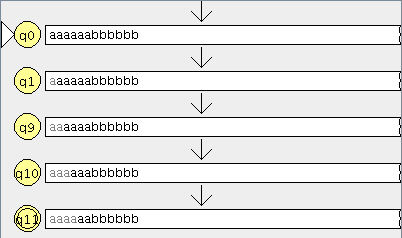
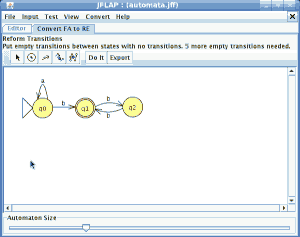
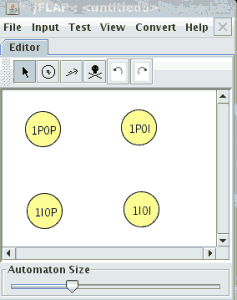
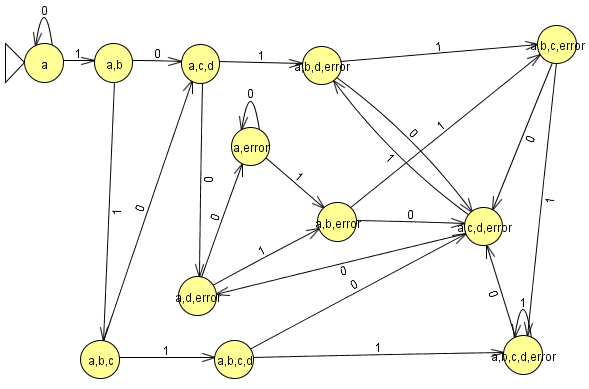
Modelamos el nuevo autómata en JFlap
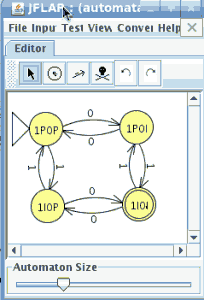
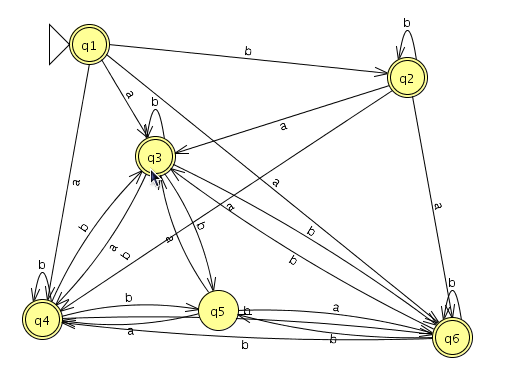 Cargamos el otro en JFlap
Cargamos el otro en JFlap
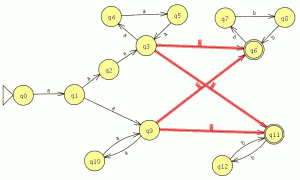
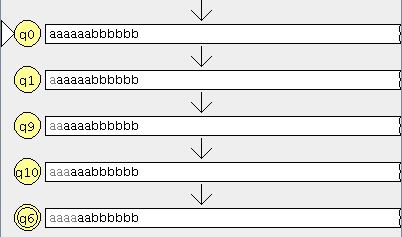
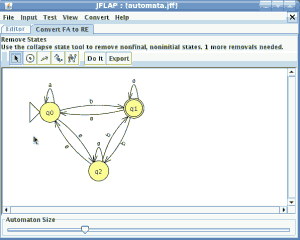
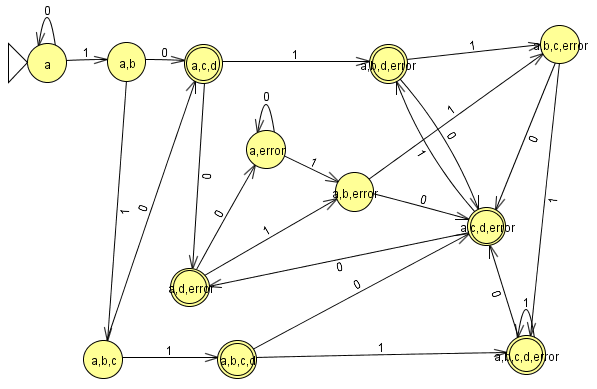
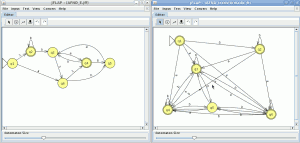 En la ventana de cualquier autómata seleccionamos el menú test y la opción “compare equivalence” y seleccionamos el otro automata
En la ventana de cualquier autómata seleccionamos el menú test y la opción “compare equivalence” y seleccionamos el otro automata
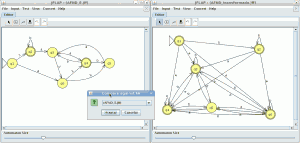
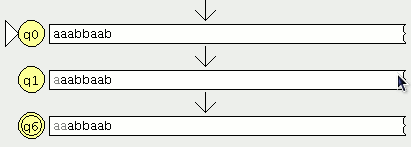
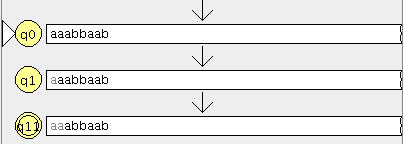
pinchamos en aceptar y son equivalentes
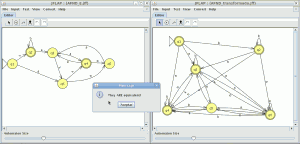 lo que significa que aceptan el mismo lenguaje
lo que significa que aceptan el mismo lenguaje
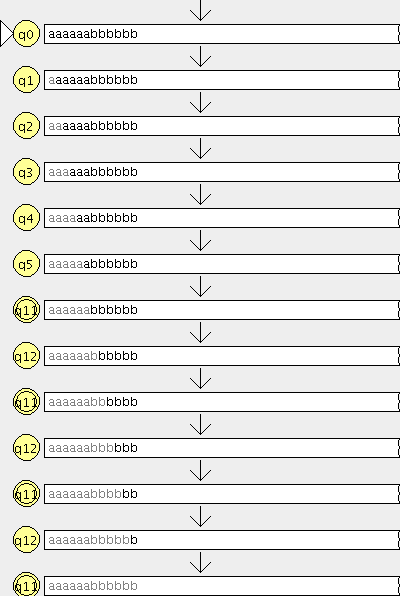
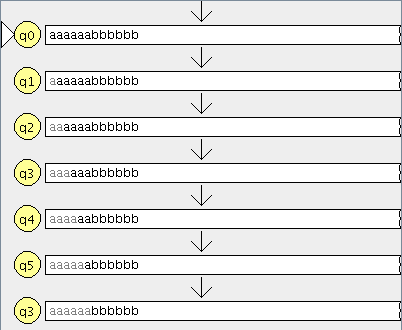
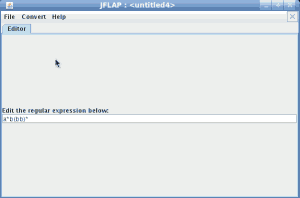
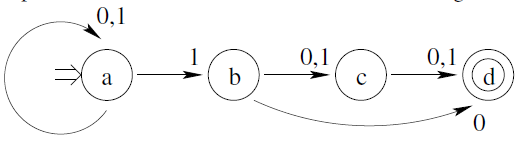
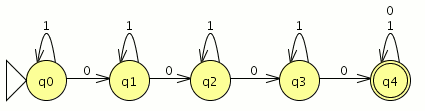 Modelar el autómata tal que acepte el lenguaje tal que
Modelar el autómata tal que acepte el lenguaje tal que ![]()
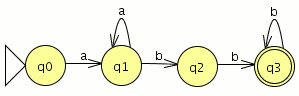 Modelar el autómata tal que acepte el lenguaje tal que
Modelar el autómata tal que acepte el lenguaje tal que ![]()
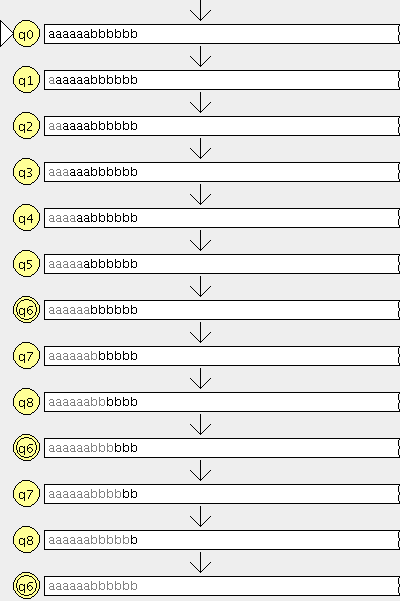
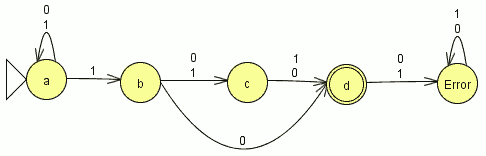
 Modelar el autómata tal que acepte el lenguaje tal que acepte todos los binarios excepto los que contengan la subcadena 101.
Modelar el autómata tal que acepte el lenguaje tal que acepte todos los binarios excepto los que contengan la subcadena 101.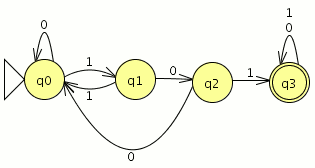 aplicamos el metodo del complemento (los estados finales se transforman en no finales y viceversa)
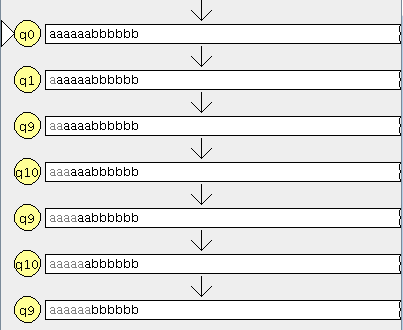
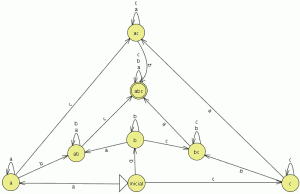
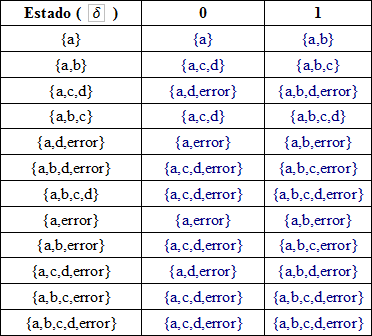
aplicamos el metodo del complemento (los estados finales se transforman en no finales y viceversa)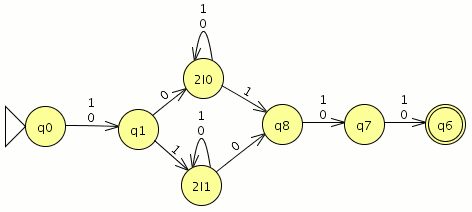 Dado un alfabeto {a, b, c}, construir un AFD que acepte aquellas palabras que contengan al menos dos ‘a’, una ‘b’ y una ‘c’
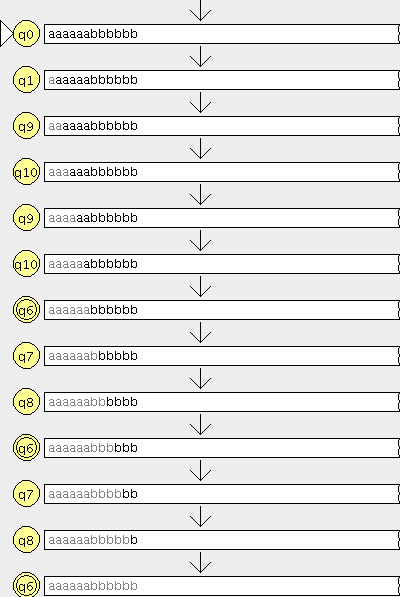
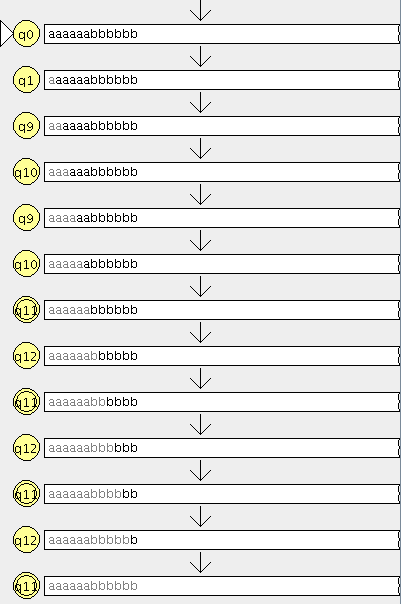
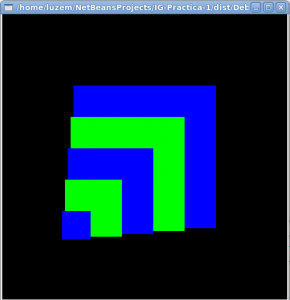
Dado un alfabeto {a, b, c}, construir un AFD que acepte aquellas palabras que contengan al menos dos ‘a’, una ‘b’ y una ‘c’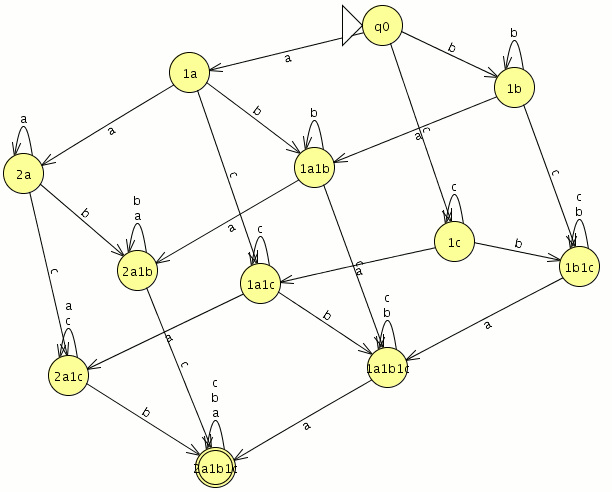 teneis aqui el Autómata
teneis aqui el Autómata