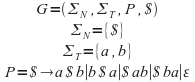Ahora que se acabaron las practicas y las hojas de talf lo único que queda son las respuestas a las preguntas de teoría y como no las tengo podíamos intentar completarlas entre todos (dejáis un comentario con la pregunta y la respuesta).
Ya están acabadas, gracias por vuestra nula colaboración
Exámen Xuño de 2005
Dado dos lenguajes regulares L1 y L2 . ¿El lenguaje de unión L1 ∪ L2 también es un lenguaje regular?
Cierto, porque L1 y L2 al ser regulares existe una expresión regular que los define cada lenguaje, dichas expresiones se pueden concatenar para generar el lenguaje que define la union.
¿Un autómata finito determinista siembre tiene un número mayor de estados que un autómata finito no–determinista asumiendo que ambos aceptan el mismo lenguaje?
Falso, sobre un autómata finito determinista podemos añadir transiciones epsilon a nuevos estados sin alterar el lenguaje que genera
¿L+ != L∗ si y solo si ∈ L?
Respuesta
¿Existen lenguajes libres de contexto que no son regulares?
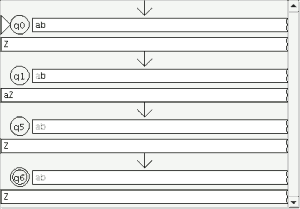
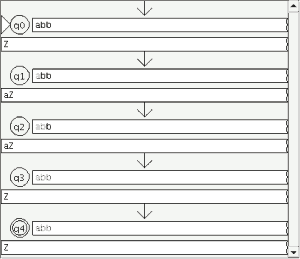
Verdadero Un lenguaje libre de contexto es generado por una gramática libre de contexto y la gramática $ -> a$b | € genera el lenguaje no regular a^nb^n : N>=0
¿Si una gramática es ambigua también el lenguaje que genera es ambiguo?
No, para que un lenguaje sea ambiguo todas las gramáticas que lo generan tienen que ser ambiguas no es suficiente con una
¿Una gramática regular puede ser ambigua?
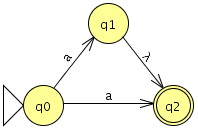
Si, por ejemplo
$ -> aA | aB
A->b
B->b (es regular y ambigua)
¿Existen expresiones regulares que definen lenguajes que no se pueden aceptar con un autómata finito con pila?
No porque para toda ER existe un AF y por definición todo AF es un AFP en el que la pila no se mueve
¿Un autómata finito con pila determinista puede realizar cambios de estados sin leer un símbolo de la entrada?
Si, siempre cuando realice una lectura ![]() y para esa lectura solo exista un camino
y para esa lectura solo exista un camino
¿Si dos expresiones regulares no son iguales, los lenguajes que definen pueden ser iguales?
¿Para L = L(α) con α = a∗ b∗ c∗ , RL tiene índice 4?
Si, el autómata mínimo completo tiene 4 estados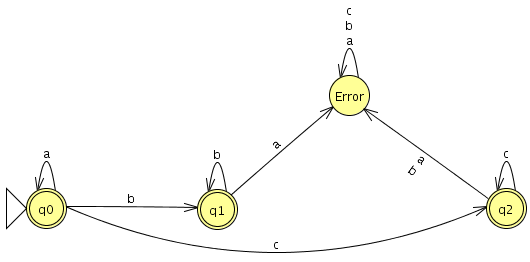
Exámen Setembro de 2005
Dado dos lenguajes regulares L1 y L2 . ¿El lenguaje de intersección L1 ∩ L2 también es un lenguaje regular?
Por las lyes de De Morgan sabemos que ![]()
![]() que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
![]() que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
![]() que es un lenguaje regular, porque la unión de dos lenguajes regulares genera un lenguaje regular
que es un lenguaje regular, porque la unión de dos lenguajes regulares genera un lenguaje regular
![]() que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
¿Un autómata finito no–determinista siempre tiene un número menor de estados que un autómata finito determinista asumiendo que ambos aceptan el mismo lenguaje?
No,
¿L+ = L∗ si y solo si ∈ L?
Respuesta
¿Existen lenguajes libres de contexto deterministas que no son regulares?
Verdadero Un lenguaje libre de contexto es generado por una gramática libre de contexto y la gramática $ -> a$b | € genera el lenguaje no regular a^nb^n : N>=0
¿Si un lenguaje es ambiguo todas las gramáticas que generan el lenguaje son ambiguas?
Sí, un lenguaje es ambiguo si todas las gramáticas que generan el lenguaje son ambiguas.
¿Una gramática regular puede ser ambigua?
Si, por ejemplo
$ -> aA | aB
A->b
B->b (es regular y ambigua)
¿Existen expresiones regulares que definen lenguajes que no se pueden aceptar con un autómata finito determinista?
No, porque toda expresión regular se puede transformar en un AFND-![]() y este en un AFD
y este en un AFD
¿Un autómata finito con pila determinista puede realizar cambios de estados sin cambiar el contenido de la pila?
Si, siempre cuando realice una lectura ![]() y para esa lectura solo exista un camino
y para esa lectura solo exista un camino
¿Expresiones regulares definen lenguajes que se pueden aceptar con un autómata finito con pila?
Si, para toda ER existe un AF y por definición todo AF es un AFP en el que la pila no se mueve
¿Para L = L(α) con α = a∗ b∗ , RL tiene índice 4?
Respuesta
Exámen Decembro de 2005
Dado un lenguaje regular L sobre el alfabeto Σ. ¿El lenguaje complementario de L, es decir, Σ∗ − L, también es un lenguaje regular?
L = L1 = Σ*−L1 es regular, porque podemos construir, dado un AFD completo M1 que acepta L1, un AFD M que acepta L simplemente ‘invirtiendo’ sus estados finales, es decir, los estados no finales de M1 serán los estados finales de M y los finales se convierten en los no finales.
¿Existen autómatas finitos no–deterministas que tengan menos estados que sus equivalentes autómatas deterministas mínimos y completos que acepten los mismos lenguajes?
Respuesta
¿La palabra vacia pertenece a cualquier lenguaje formal?
No, porque ![]() tiene que pertenecer al subconjunto de las palabras
tiene que pertenecer al subconjunto de las palabras
¿Existen lenguajes libres de contexto deterministas que no sean regulares?
Verdadero Un lenguaje libre de contexto es generado por una gramática libre de contexto y la gramática $ -> a$b | € genera el lenguaje no regular a^nb^n : N>=0
¿Una gramática libre de contexto puede ser ambigua?
Si,
¿Un lenguaje libre de contexto puede ser ambiguo?
Sí, solo podemos afirmar que no son ambiguos los lenguajes regulares. Para que sea ambiguo todas las gramaticas que lo generan deben ser ambiguas
¿Si dos expresiones regulares son diferentes, entonces obviamente definen lenguajes regulares diferentes?
No, dos expresiones regulares pueden definir el mismo lenguaje ![]()
¿Si un lenguaje es finito, entonces es regular?
Si porque podemos construir un AF que lo genere con un camino para cada palabra que genere ese lenguaje , entonces el lenguaje es regular.
¿Un autómata finito con pila determinista puede realizar cambios de estados sin cambiar el contenido de la pila?
Si, siempre cuando realice una lectura ![]() y para esa lectura solo exista un camino
y para esa lectura solo exista un camino
¿Se puede averiguar si cualquier dos gramáticas de tipo 3 que tienen sistemas de producciones diferentes generan el mismo lenguaje regular?
Sí, obteniendo los AFD-min de ambas gramaticas y comprobando si son iguales generan el mismo lenguaje.
Exámen Xuño de 2006
Dado cualquier gramática G. ¿Se puede hallar siempre una gramática G ambigua que genera el mismo lenguage que G?
Si, porque en toda gramática no ambigua se pueden introducir producciones redundantes para generar una gramática ambigua equivalente
¿Existe una expresión regular que define un lenguaje que se puede aceptar con un autómata finito con pila?
Sí, si tenemos una ER tenemos un AF y por definición un AF es un AFP en el que la pila no se mueve.
Sea ε ∈ L y M un AFND–ε con L(M ) = L. ¿Entonces el estado inicial de M necesariamente es un estado final?
No porque al ser un AFND–ε se puede pasar de un estado a otro sin consumir nada (consumiendo solo ε ) Si fuese AFD o AFND la respuesta seria Si .
¿El AFD mínimo que acepta L tiene tantos estados finales que hay clases de equivalencia de RL que cubren L, (es decir, si unimos las palabras de dichas clases, obtenemos justamente L)?
Respuesta
¿Si Indice(RL ) = ∞, entonces L no es libre de contexto?
Respuesta
Exámen Setembro de 2006
¿Existe un lenguaje regular ambiguo?
Todo lenguaje regular puede ser definido por un AFD-mínimo y un AFD-mínimo se puede transformar en una gramática lineal no ambigua
Sean x, y, y w palabras sobre algún alfabeto. Si x es prefijo de w, e y es sufijo de w y x = y, entonces x = y = w, ¿es verdad?
falso,
Si todos los n > 1 estados de un AFD (autómata finito determinista) completo son estados finales, entonces el AFD no es mínimo.
Si porque al aplicar el algoritmo de minimización todas las casillas quedarian sin marcar por lo que todos los estados serian equivalentes.
Nota : Si en el enunciado no apareciese completo seria Falso.
¿La concatenación de dos lenguajes libres de contexto produce de nuevo un lenguaje libre de contexto?
Respuesta
¿Se puede averiguar si una gramática libre de contexto G genera alguna palabra, es decir, averiguar si L(G) = ∅?
Si comprobando que $ es generativo.
Exámen Decembro de 2006
¿Existe un lenguaje libre de contexto ambiguo?
Respuesta
Sean x, y, y w palabras sobre algún alfabeto. Si x es prefijo de w, e y es sufijo de w y x = y, entonces x = y = w, ¿es verdad?
Respuesta
Si todos los estados de un AFD (autómata finito determinista) completo M son estados finales, entonces el Indice(RL(M ) ) = 1?
Sí, porque en el algoritmo de minimización todas las casillas quedarían sin marcar , siendo todos equivalentes , quedando un solo estado.
¿La intersección de dos lenguajes regulares produce de nuevo un lenguaje regular?
Por las lyes de De Morgan sabemos que ![]()
![]() que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
![]() que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
![]() que es un lenguaje regular, porque la unión de dos lenguajes regulares genera un lenguaje regular
que es un lenguaje regular, porque la unión de dos lenguajes regulares genera un lenguaje regular
![]() que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular
¿Se puede averiguar si una gramática libre de contexto G genera la palabra vacía, es decir, averiguar si ε ∈ L(G)?
Respuesta
Exámen Xuño de 2007
Si existe una gramática lineal por la izquierda G que genera un lenguaje formal L, entonces L es finito. ¿Es correcto?
No
S -> aB
B -> aB | a
Si una expresión regular no contiene ningún asterisco (de Kleene), entonces el lenguaje es finito. ¿Es correcto?
No, puede contener el operador ⁺
Si un autómata finito determinista mínimo tiene dos estados finales, entonces adicionalmente tiene también por lo menos un estado no final. ¿Es correcto?
Si, porque si son todos estados finales el autómata mínimo estaría compuesto por un único estado final
¿Un autómata finito con pila (no–determinista) que nunca vacía su pila puede aceptar alguna palabra?
Si, por estado final
¿Dada una gramática lineal por la derecha ambigua G, es posible construir una grámatica lineal por la izquierda no–ambigua G que genera el mismo lenguaje, es decir, con L(G ) = L(G)?
Una gramática lineal genera un lenguaje regular y sobre un lenguaje regular se puede generar un autómata y sobre este obtener una gramática lineal por la izquierda no ambigua
Exámen Setembro de 2007
Sean $ −→∗ w y $ −→∗ w dos derivaciones distintas para una palabra w ∈ L ⊂ {a, b, c}∗ y una gramática G con L(G) = L. ¿El lenguage L entonces es ambiguo?
Respuesta
¿Si la unión y el complemento son operaciones cerradas para un tipo de lenguajes formales, entonces la intersección también es una operación cerrada para este tipo?
Respuesta
Para cualquier lenguaje regular L existe un AFND– M con L(M ) = L que contiene un solo estado final. ¿Es correcto?
Si, porque sobre el AFD podemos crear un nuevo estado final incluir transiciones ![]() desde el resto de estados finales y transformar los otros estados finales en no finales
desde el resto de estados finales y transformar los otros estados finales en no finales
Si un autómata finito determinista mínimo tiene dos estados finales, entonces adicionalmente tiene también por lo menos un estado no final. ¿Es correcto?
Respuesta
Una gramática en Forma Normal de Chomsky nunca puede ser ambigua. ¿Es correcto?
Respuesta
Examen Junio de 2008
Sea L un lenguaje regular y ![]() , es decir, L1 contiene un subconjunto de las palabras de L. ¿El lenguaje L1 entonces es necesariamente regular?
, es decir, L1 contiene un subconjunto de las palabras de L. ¿El lenguaje L1 entonces es necesariamente regular?
No, ![]() es regular y L1 puede ser libre de contexto
es regular y L1 puede ser libre de contexto
Si dos autómatas finitos deterministas son equivalentes, entonces tienen el mismo numero de estados finales. ¿es correcto?
No.
Si un autómata finito determinista mínimo tiene cuatro estados , por lo menos uno de ellos es un estado no final. ¿Es correcto?
Si, porque si fueran todos finales en la minimización quedaría un único estado final equivalente
Una gramática en Forma Normal de Chomsky puede ser ambigua. ¿Es correcto?
Si, ejemplo:
Examen Diciembre de 2008
¿Existe un lenguaje regular ambiguo?
Un lenguaje ambiguo es aquel que todas las gramáticas que lo generan son ambiguas, pero para todo lenguaje regular se puede crear un AFD mínimo de que obtenemos una gramática no ambigua
Sean x,y, y w palabras sobre algún alfabeto. Si x e y son prefijos de w, entonces x es prefijo y, ¿es verdad?
No,
y=a
x=ab
w=abc
Si todos los estados de un AFD (autómata finito determinista) completo M son estados finales, entonces el Indice(RL(M)) =1?
Si porque al aplicar el algoritmo de minimización quedaría un único estado final equivalente
¿La unión de dos lenguajes libres de contexto produce de nuevo un lenguaje libre de contexto?
Si partimos de las gramáticas que generan los lenguajes dos lenguajes libres de contexto L1 y L2 podemos crear una nueva gramática donde su símbolo inicial enlace los dos lenguajes $ -> $L1 | $L2
¿Se puede averiguar si una gramática libre de contexto G genera alguna palabra, es decir, averiguar si ![]() ?
?
Si, comprobando que el símbolo inicial es generativo.
Examen Junio de 2009
Sea L un lenguaje regular. ¿Existe una gramática lineal por la derecha G que genera L, es decir, L(G)=L, y cuyo numero de variables es igual a Indice(RL)?
Si. Un lenguaje regular es aceptado por un AFD mínimo, con un numero de estados igual al Indice(RL). Al convertir el AFD mínimo en una gramática lineal por la derecha, cada estado sera una variable.
Si una expresión regular contiene un asterisco (de Kleene), entonces el lenguaje es infinito. ¿Es correcto?
No.
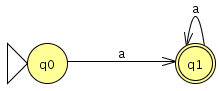
Si un autómata finito determinista mínimo (completo) tiene un solo estado no final (a parte de sus estados finales), entonces dicho estado no final (si lo dibujamos) tiene una arista reflexiva. ¿Es correcto?
No. Ejemplo:
¿Para cada autómata finito con pila no determinista (AFPND) que acepta con estado final existe una AFPND que acepta con pila vacía?
Si , porque un AFPND que acepta con pila vacía se puede transformar en AFPND que acepta en estado final y viceversa usando el método de la simulación.
¿Dada una gramática lineal por la derecha ambigua G, es posible construir una gramática lineal por la derecha no ambigua G’ que genera el mismo lenguaje, es decir, con L(G’)=L(G)?
Si. Una gramática lineal por la derecha genera un lenguaje regular y un lenguaje regular se puede modelar con un AFD mínimo , este AFD mínimo puede ser convertido en una gramática lineal por la derecha no ambigua.
Examen Septiembre de 2009
Sea L un lenguaje regular. ¿Existe una gramática lineal por la derecha G que genera L, es decir, L(G)=L, y cuyo numero de variables es igual a Indice(RL)+5?
Si. Un lenguaje regular es aceptado por un AFD mínimo, con un numero de estados igual al Indice(RL). Al convertir el AFD mínimo en una gramática lineal por la derecha, cada estado sera una variable. Sobre esta gramática, podemos añadir el numero de variables redundantes que queramos, en este caso 5.
Si una expresión regular contiene un asterisco (de Kleene), entonces el lenguaje es infinito. ¿Es correcto?
No.
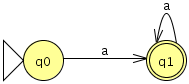
Si un autómata finito determinista mínimo (completo) tiene un solo estado no final (a parte de sus estados finales), entonces dicho estado no final (si lo dibujamos) tiene una arista reflexiva. ¿Es correcto?
No. Ejemplo:
¿Para cada autómata finito con pila no determinista (AFPND) que acepta con pila vacía existe una AFPND que acepta en estado final?
Si , porque un AFPND que acepta con pila vacía se puede transformar en AFPND que acepta en estado final y viceversa usando el método de la simulación.
¿Dada una gramática lineal por la izquierda ambigua G, es posible construir una gramática lineal por la derecha no ambigua G’ que genera el mismo lenguaje, es decir, con L(G’)=L(G)?
Si. Una gramática lineal por la izquierda genera un lenguaje regular y un lenguaje regular se puede modelar con un AFD mínimo , este AFD mínimo puede ser convertido en una gramática lineal por la derecha no ambigua.
Examen Diciembre de 2009
Sea L un lenguaje regular ¿Existe una gramática lineal por la derecha G que genera ![]() ?
?
Si, Si L es regular podemos crear un AFD que acepta el lenguaje, sobre ese AFD aplicando el método del complemento obtenemos un AFD que acepta![]() y a partir de este ultimo AFD podemos crear una gramática linear por la derecha que genera
y a partir de este ultimo AFD podemos crear una gramática linear por la derecha que genera ![]()
Si una expresión regular contiene el un asterisco (de Kleene), entonces el lenguaje es infinito. ¿Es correcto?
No.
¿Que se entiende bajo el concepto que una operación entre lenguajes sea una operación cerrada?
Los lenguajes son un tipo de conjuntos. Que una operación sea cerrada quiere decir que cuando esta operación se aplica a elementos de ese conjunto, en este caso a un lenguaje, el resultado sigue estando en ese conjunto, es decir, sigue siendo un lenguaje. Ejemplo: ![]() es un lenguaje regular si A,B son lenguajes regulares.
es un lenguaje regular si A,B son lenguajes regulares.
Sea L un lenguaje libre de contexto. ¿Existe un lenguaje L’ tal que ![]() sea regular?
sea regular?
Si, ![]() es regular y si L es libre de contexto
es regular y si L es libre de contexto ![]() por lo tanto para todo lenguaje L libre de contexto la unión con su complemento genera un lenguaje regular
por lo tanto para todo lenguaje L libre de contexto la unión con su complemento genera un lenguaje regular
¿Dada una gramática lineal por la izquierda ambigua G, es posible construir una gramática lineal por la derecha no ambigua G’ que genera el mismo lenguaje, es decir, con L(G’)=L(G)?
Si. Una gramática lineal por la izquierda genera un lenguaje regular y un lenguaje regular se puede modelar con un AFD mínimo , este AFD mínimo puede ser convertido en una gramática lineal por la derecha no ambigua.
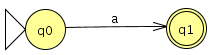
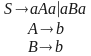
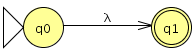
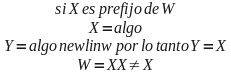
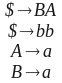










 opci
opci