Hoja 9 (27 de Abril de 2010)

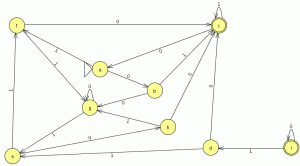
P1: Minimiza el siguiente autómata finito determinista. El estado inicial es el estado a.

Paso 1: eliminamos estados no accesibles.

Un estado no accesible es un estado que no esta relacionado con el conjunto de estados al que pertenece el estado inicial o perteneciendo a este no tiene símbolos de entrada solo de salida. en este caso eliminamos el elemento i, al eliminar el estado i el estado d queda sin símbolos de entrada por lo tanto d tampoco es accesible.

Paso 2: construimos la matriz de estados

matriz de estados

X/X	^a	b	*c		e	f	g	h
^a	“”	“”	“”		“”	“”	“”	“”
b	“”	“”	“”		“”	“”	“”	“”
*c	“”	“”	“”		“”	“”	“”	“”
e	“”	“”	“”		“”	“”	“”	“”
f	“”	“”	“”		“”	“”	“”	“”
g	“”	“”	“”		“”	“”	“”	“”
h	“”	“”	“”		“”	“”	“”	“”

cada estado es equivalente entre si por lo tanto los descartamos de la misma forma que un triangular de la matriz

X/X	^a	b	*c		e	f	g	h
^a	~	“”	“”		“”	“”	“”	“”
b	~	~	“”		“”	“”	“”	“”
*c	~	~	~		“”	“”	“”	“”
e	~	~	~		~	“”	“”	“”
f	~	~	~		~	~	“”	“”
g	~	~	~		~	~	~	“”
h	~	~	~		~	~	~	~

un estado no final no va a ser equivalente a un estado no final por lo tanto marcamos las celdas donde se relacione un estado final y uno no final

X/X	^a	b	*c		e	f	g	h
^a	~	“”	X		“”	“”	“”	“”
b	~	~	X		“”	“”	“”	“”
*c	~	~	~		X	X	X	X
e	~	~	~		~	“”	“”	“”
f	~	~	~		~	~	“”	“”
g	~	~	~		~	~	~	“”
h	~	~	~		~	~	~	~

llegados a este punto comenzamos a emparejar los estados no marcados:

• (a,b) X
  • con 0 vamos a (b,g) no esta marcado no hacemos nada
  • con 1 vamos a (f,c)  esta marcado por lo tanto marcamos (a,b)
• (a,e) X
  • con 0 vamos a (b,h)  esta en la diagonal principal no hacemos nada
  • con 1 vamos a (f,f)   esta en la diagonal principal no hacemos nada
  • quedamos a la espera de lo que suceda cuando miremos (b,h)
• (a,f) X
  • con 0 vamos a (b,c) como esta marcado marcamos (a,f)
  • con 1 vamos a (f,g) como no esta marcado no hacemos nada
• (a,g) X
  • con 0 vamos a (b,g) como no esta marcado ni no comprobado esperamos a lo que suceda al comprobar (b,g)
  • con 1 vamos a (f,e) que no esta marcado no hacemos nada
• (a,h) X
  • con 0 vamos a (b,c) como esta marcado marcamos (a,h)
  • 1 no lo miramos porque (a,h) ya se ha marcado
• (b,e) X
  • con 0 vamos a (g,h) como no esta marcado no hacemos nada.
  • con 1 vamos a (c,f) como esta marcado marcamos (b,e)
• (b,f) X
  • con 0 vamos a (g,c) como (c,g) esta marcado marcamos (b,f)
  • 1 no lo miramos porque (b,f) ya se ha marcado.
• (b,g) X
  • con 0 vamos a (g,g) como esta en la diagonal principal no hacemos nada
  • con 1 vamos a (c,e) como esta marcado marcamos (b,g)
  • (a,g) estaba a la espera de (b,g) como (b,g) se ha marcado también marcaremos (a,g)
• (b,h) X
  • con 0 vamos a (g,c) como (c,g) ya esta marcado marcamos (b,h)
  • 1 no lo miramos porque (b,h) ya se ha marcado
  • (a,e) estaba a la espera de (b,h) como lo hemos marcado marcamos también (a,e)
• (e,f) X
  • con 0 vamos a (h,c)  como (c,h) esta marcado marcamos (e,f)
  • 1 no lo miramos porque (e,f) ya esta marcado
• (e,g) X
  • con 0 vamos a (h,g) o (g,h) como no esta marcado ni comprobado esperamos a comprobar (g,h)
  • con 1 vamos a (f,e) o (e,f) como  esta marcado marcamos (e,g)
  • marcamos también (d,f) y (d,h) porque estaban a la espera de (e,g)
• (e,h) X
  • con 0 vamos a (h,c) como (c,h) esta marcado marcamos (e,h)
  • 1 no lo miramos porque (e,h) ya se ha marcado
• (f,g) X
  • con 0 vamos a (c,g) como ya esta marcado marcamos (f,g)
  • 1 no lo miramos porque ya hemos marcado (f,g)
• (f,h)
  • con 0 vamos a (c,c) como esta en la diagonal principal lo obviamos
  • con 1 vamos a (g,g) como esta en la diagonal principal lo obviamos
• (g,h) X
  • con 0 vamos a (g,c) como (c,g) esta marcado marcamos (g,h)
  • 1 no lo miramos porque ya hemos marcado (g,h)

Finalmete la matriz queda de la siguiente forma

X/X	^a	b	*c		e	f	g	h
^a	~	X	X		X	X	X	X
b	~	~	X		X	X	X	X
*c	~	~	~		X	X	X	X
e	~	~	~		~	X	X	X
f	~	~	~		~	~	X	“”
g	~	~	~		~	~	~	X
h	~	~	~		~	~	~	~

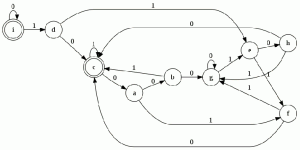
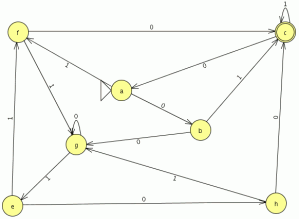
las casillas no marcadas indican estados equivalentes en este caso solo tenemos una casilla no marcada que es (f,h) que nos indica que f es equivalente a h quedando el autómata mínimo de esta forma:

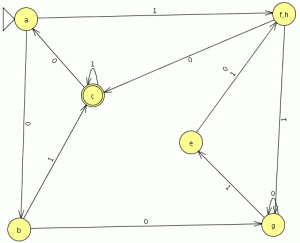
nuestro autómata mínimo esta formado por 7 estados  para comprobar si la minimización  esta bien realizada minimizamos el automata original en JFlap y comparamos su equivalencia y el numero de estado del autómata mínimo generado, el automata minimo generado es el siguiente:

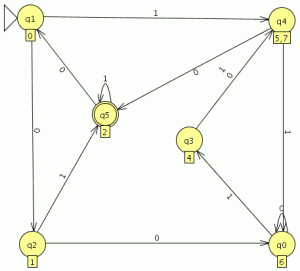el numero de estados es el mismo el los dos autómatas y el lenguaje generado es equivalente  por lo que debería de estar bien

P2: Determina el Indice(RL) del lenguaje definido por una expresión regular sobre el alfabeto {a, b, c} que define todas las palabras que tengan por lo menos dos a’s consecutivas o por lo menos dos b’s consecutivas (mira hoja 6 si quieres).

Para saber el indice  (RL) de la expresión regular  tenemos que realizar el siguiente proceso de conversión
Expresión Regular –> AFND-ε –> AFND —> AFD —> AFD mínimo

la expresión regular es (a + b + c)∗ (aa + bb)(a + b + c)∗

el numero de estados del AFD minimo sera el indice del RL en caso que sea completo sino tenemos que sumarle 1 por el estado de error

Paso 1 Expresión Regular a AFND-ε:
Para realizar esta conversión nos basamos en los cinco casos básicos:

• caso 1:para caso “A”
• regla 2:para caso  “epsilon”
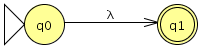
• regla 3:para caso “AB”
• regla 4:para caso “A+B”
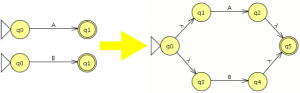
• regla 5:para caso “A*”

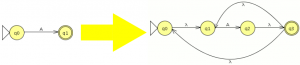
Dividimos la expresión regular en los subconjuntos mínimos a generando un árbol de descomposición.

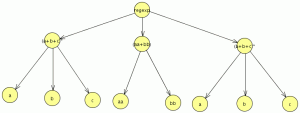empezamos a modelar desde el segundo nivel ya que el primero es muy sencillo

(a+b+c)*

(aa+bb)

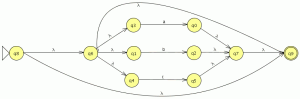
unimos los autómatas del segundo nivel y generaremos el automata que describe la expresión regular (a + b + c)∗ (aa + bb)(a + b + c)∗.

comparamos con el JFlap y son equivalentes por lo tanto este paso va bien, ahora eliminamos las transiciones epsilon.

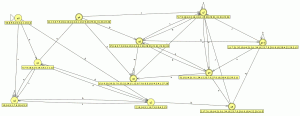Y el AFD generado lo minimizamos

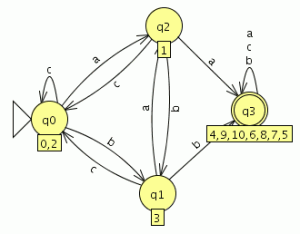como es completo el indice(RL) es igual a 4 , si no fuera completo habría que añadir el estado de error siendo el indice(RL) igual al numero de estados del AFD mínimo + el estado de error