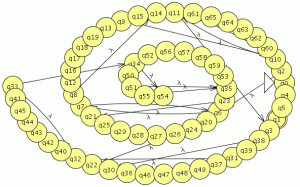
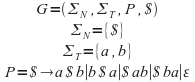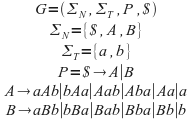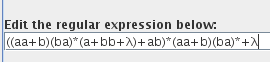1. Comprobar si son equivalentes:
a)
- S -> aaS
- S -> bB
- B -> bB
- B -> b
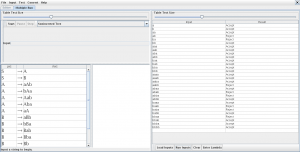
b)
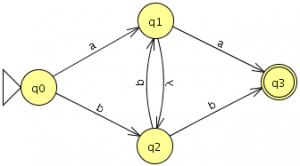
c)
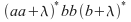
para compara si los anteriores elementos debemos transformar la expresión regular y la gramática en una expresión regular
para la expresión regular los pasos son los siguientes :
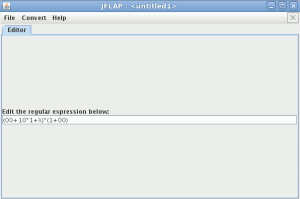
Abrimos el JFlap y seleccionamos la Opción “Regular Expression”

insertamos la expresión regular en el JFlap λ
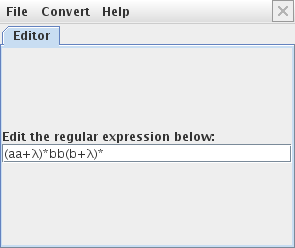
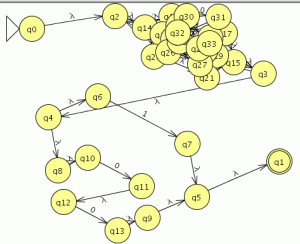
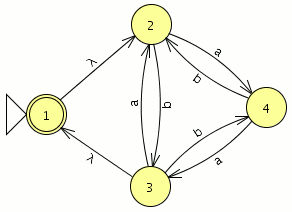
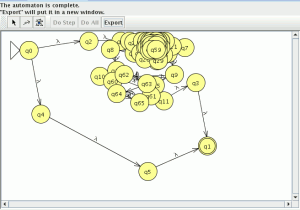
Ahora la convertimos en un autómata con la opción “Convert NFA” del menú “convert”
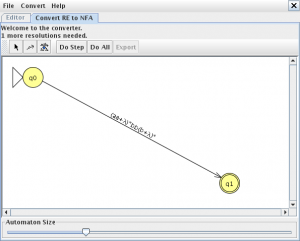
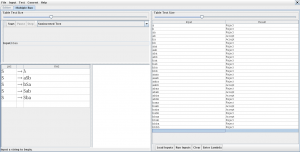
pinchamos en “Do All” y “Export” lo que nos mostrara una nueva ventana con el autómata equivalente a la expresión regular
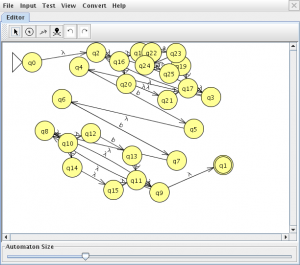 guardamos el autómata generado para compararlo después .
guardamos el autómata generado para compararlo después .
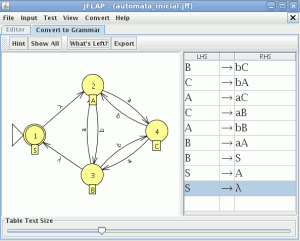
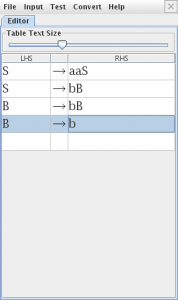
Seguidamente modelamos la gramática en JFlap para ello abrimos el JFlap y seleccionamos la opción “Grammar”
 modelamos la gramática en la nueva ventana
modelamos la gramática en la nueva ventana
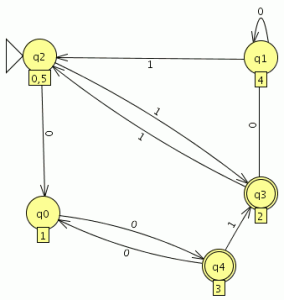
 como es una gramática lineal por la derecha seleccionamos la opción “Convert Right Lineal Grammar to FA” en el menú “Convert”
como es una gramática lineal por la derecha seleccionamos la opción “Convert Right Lineal Grammar to FA” en el menú “Convert”
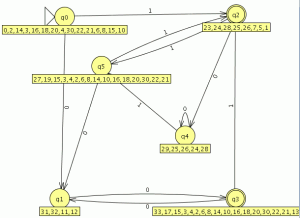
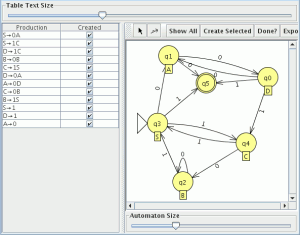
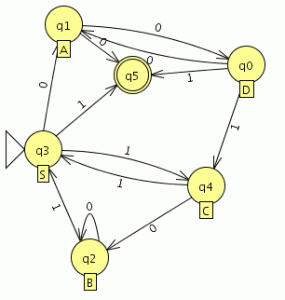
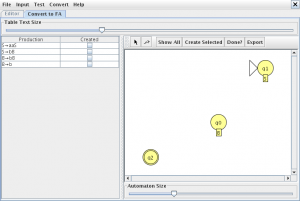 pinchamos en “Show All” y “Export” lo que nos creara un autómata equivalente a la gramática
pinchamos en “Show All” y “Export” lo que nos creara un autómata equivalente a la gramática
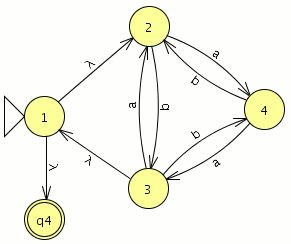
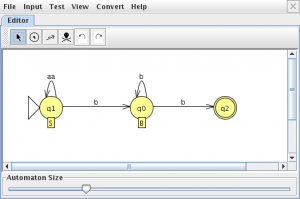 ahora con los tres autómatas abiertos vamos a comparar equivalencias
ahora con los tres autómatas abiertos vamos a comparar equivalencias
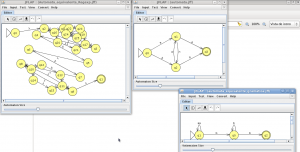
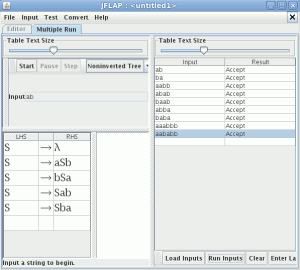
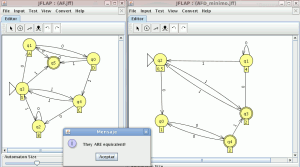
Para comparar la equivalencia entre autómatas seleccionamos la opción “Compare Equivalence” en el menú “Test” lo que nos preguntara con que autómata queremos comparar
El resultado es: La gramática y la expresión regular son equivalentes
2. Dada a seguinte gramática
- A -> CB2
- A -> 1B
- A -> ε
- B -> BC
- B ->1
- C -> 2
a) Transformar a forma normal de Chomsky
modelamos la gramática en JFLAP
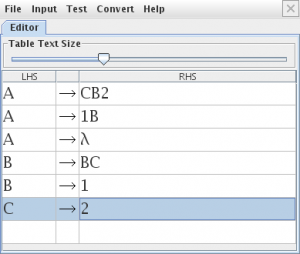 Para convertirla a Chomsky seleccionamos la opción “Transform Grammar” en el menú “Convert“, nos advierte que eliminara el símbolo Lambda
Para convertirla a Chomsky seleccionamos la opción “Transform Grammar” en el menú “Convert“, nos advierte que eliminara el símbolo Lambda
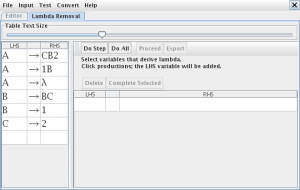 pinchamos en “Do All” y “Procceed” y se creara una nueva pestaña
pinchamos en “Do All” y “Procceed” y se creara una nueva pestaña
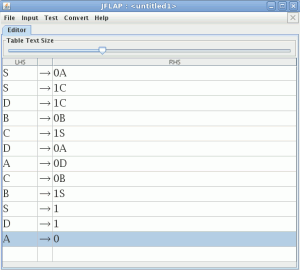
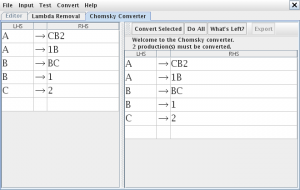 Pinchamos en “Do All” y “Export” y aparecerá la gramática convertida a forma normal de Chomsky
Pinchamos en “Do All” y “Export” y aparecerá la gramática convertida a forma normal de Chomsky
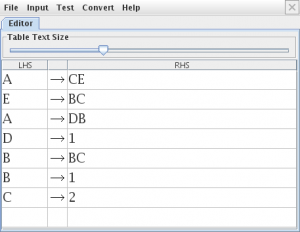
b) Convertir a resultante a un autómata de pila polo método LL
Sobre la gramática generada pinchamos en la opción “Convert CFG to PDA (LL)” en el menú “Convert” nos abrirá una nueva pestaña
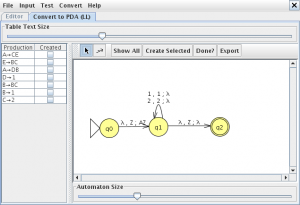
pinchamos en “Show All” y “Export” lo que nos mostrara el autómata de pila
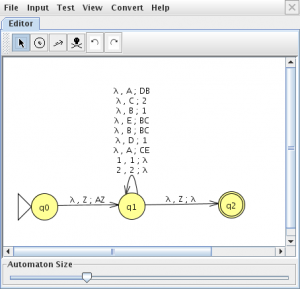 c) Obten a traza para a cadea de entrada 1122
c) Obten a traza para a cadea de entrada 1122
Menú “Input” opción “Step by State” abre un dialogo insertamos la cadena 1122 y seleccionamos Final State
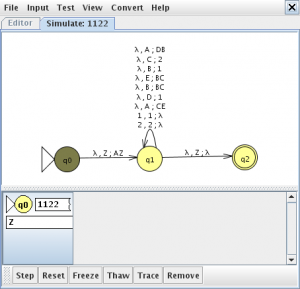 le damos a step hasta que aparezca un estado en verde lo seleccionamos y pinchamos en trace la traza final es la siguiente:
le damos a step hasta que aparezca un estado en verde lo seleccionamos y pinchamos en trace la traza final es la siguiente:

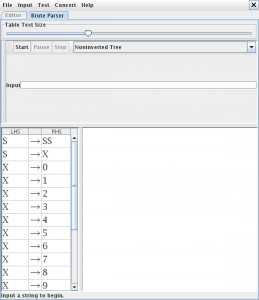
![]() abrimos el JFlap y pinchamos en la opción “Grammar”
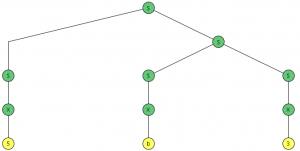
abrimos el JFlap y pinchamos en la opción “Grammar”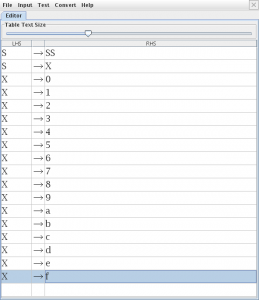 para generar el árbol de derivación utilizamos la opción “Brute Force Parse” en el menú “Input” que nos abrirá una nueva pestaña
para generar el árbol de derivación utilizamos la opción “Brute Force Parse” en el menú “Input” que nos abrirá una nueva pestaña