P1: Construye una gramática libre de contexto G que genera todas las palabras sobre el alfabeto {a, b} que tienen el mismo número de a’s y b’s, es decir,
L(G) = {ε, ab, ba, aabb, abab, baab, abba, baba, bbaa, aaabbb, aababb, . . .}
La gramática a generada es la siguiente:
abrimos el JFlap y comprobamos si acepta las palabras del lenguaje
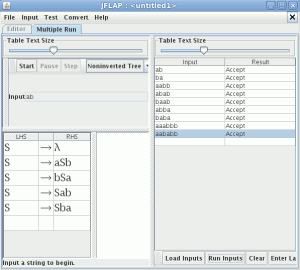 generamos un archivo con diversas palabras con los caracteres a y b para verificar que no acepta las palabras que no cumplen la regla
generamos un archivo con diversas palabras con los caracteres a y b para verificar que no acepta las palabras que no cumplen la regla
P2: Construye una gramática libre de contexto G que genera todas las palabras sobre el alfabeto {a, b} que tienen un número diferente de a’s y b’s (ayuda: amplía la gramática del primer punto).
Para construir esta gramatica nos basaremos en las producciones anteriores evitando la producción de la palabra vaciá y dividiendo el problema en dos grupos palabras con mayor numero de letras a que de b (A) y palabras con mayor numero de letras b que de a (B). para ello simplemente evitaremos que las producciones terminales de A y B generen ε y permitan introducir un numero ilimitado de as y de bes.
verificamos algunas palabras en el JFlap
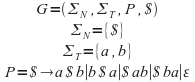
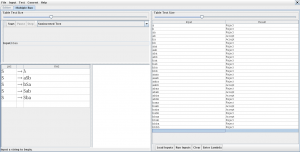
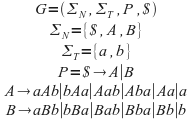
Hola!!! Es posible que haya mas de una solución??? Porque a mi me ha salido otra gramática y me acepta las mismas palabras que a ti xD Un saludo.
Si, puede existir mas de una solución porque diferentes gramáticas pueden generar el mismo lenguaje
Ok!!! Muchisimas gracias xD
Cuidado, esta gramática que propone luzem para el problema P1 es incorrecta, no genera todas las cadenas, por ejemplo aabbbbaa.
El mismo problema lo “hereda” la que propone para P2
Aabbbaa tiene 3b y 2a por lo tanto no tiene el mismo numero de as y bes