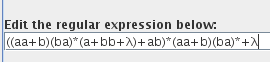regexp – La Fabulosa Vida de un IT

03/05/2011

Using Logical Or in Perl regex


#!/usr/bin/perl

use strict;
use warnings;

my %colors=( "life" , "white or black",
 "cat" , "black",
 "horse" , "white or black",
 "blood",    "red",
 "sky" ,"blue");

foreach my $coloredThing (keys %colors)
{
 print "$coloredThing ";
 if ($colors{$coloredThing}=~m/(black|white)/)
 {
 print "Match";
 }
 else
 {
 print "Doesn't Match";
 }
 print "\n";
}

and here the Output

sky Doesn’t Match
blood Doesn’t Match
cat Match
horse Match
life Match

27/04/2010

Practica 7 Conversiones Autómatas lenguajes regexp en JFlap

El enunciado de la practica aqui:Practica 7 TALF

1.-Encuentra el AFD mínimo que reconoce el lenguaje representado por la expresión regular (RegEx) siguiente (00+10*1+λ)*(1+00)

En JFlap escogemos la opción de expresión regular

introducimos la expresión regular en el cuadro de dialogo

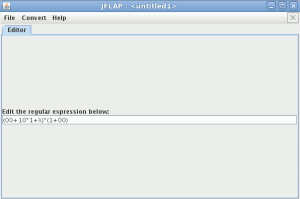
seleccionamos la opción Convert to NFA del menu convert para convertir una expresión regular en un autómata finito no determinista lo que nos creara el siguiente AFND

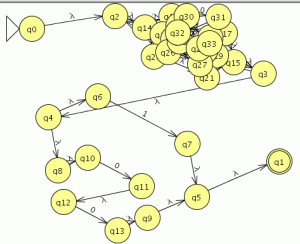Convertimos el AFND en un AFD usando la opción “Convert to DFA” del menú Convert

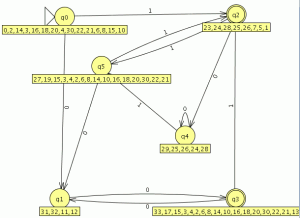como ultimo paso debemos minimizar el autómata finito determinista la opción para realizar la minimización se encuentre en el menú Convert en la opción minimize DFA

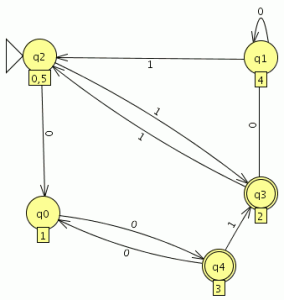
2.-Encuentra el AFD mínimo que reconoce el lenguaje representado por la siguiente gramática, y comprueba si es equivalente al del ejercicio anterior

S → 0A
S → 1C
D → 1C
B → 0B
C → 1S
D → 0A
A → 0D
C → 0B
B → 1S
S →1
D→1
A→0

Introducimos la gramática en JFlap

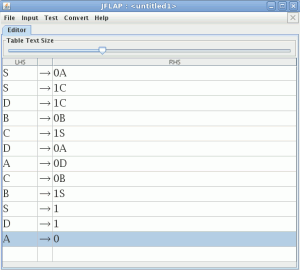
Pinchamos en Convert –> Convert Right Lineal Grammar to FA nos aparece una ventana donde introducimos la siguiente secuencia Show all -> Done? –> Export

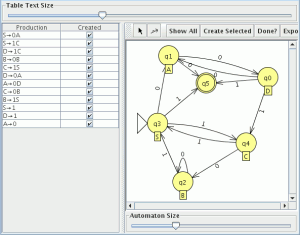
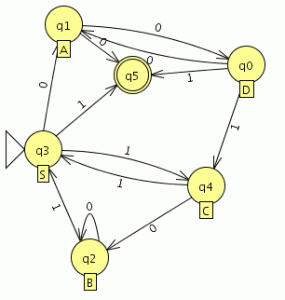
Aparece una nueva Ventana con el FA generado

Seleccionamos el menu test -> compare equivalence –> seleccionamos el AFD minimo del apartado anterior

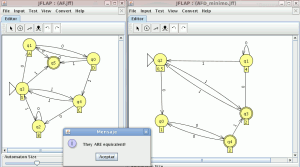
son equivalentes

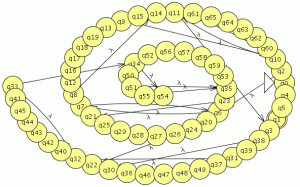
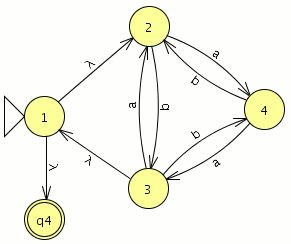
3.-Encuentra una expresión regular y una gramática para el lenguaje reconocido por el autómata siguiente

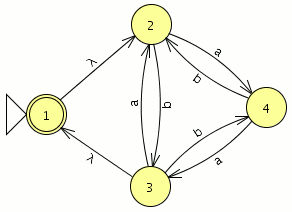para convertir el autómata en una expresión regular seleccionamos la opción “convert FA to RE” del menú “convert” que nos obligara a añadir un estado final que no sea inicial quedando de la siguiente forma

pinchamos en el botón “Do It” hasta que realice todos los pasos necesarios para la conversión informándonos en este punto con un mensaje con el siguiente text “You’re done. Go away.” momento en el que pincharemos en export que nos mostrara la expresión regular en una nueva ventana.

(b(ab)*+(a+b(ab)*(b+aa))(ba+(a+bb)(ab)*(b+aa))*(a+bb)(ab)*)*

para convertir el autómata en una gramática en la ventana del autómata seleccionamos “Convert to Grammar” en el menú “Convert” y presionamos repetidamente el botón “Hint” repetidas veces hasta que genere la gramática

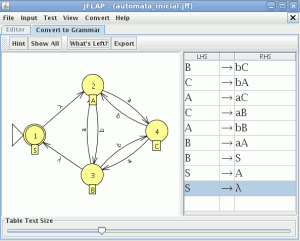
una vez generada la gramática solo resta pulsar en el botón Export que abrirá una nueva ventana con la gramática

4.-Comprueba que el autómata anterior es equivalente a la siguiente Expresión Regular ((aa+b)(ba)*(a+bb+λ)+ab)*(aa+b)(ba)*+λ

JFlap no puede compara equivalencia entre expresiones regulares por lo tanto debemos transformar la expresión regular en un autómata para eso creamos una nueva expresión regular en JFlap

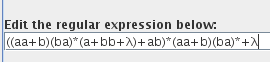
una vez insertada la expresión regular seleccionamos la opción “Convert to NFA” del menú “Convert”

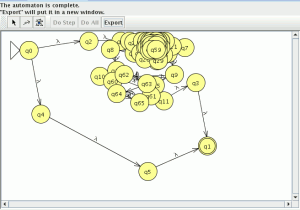
Una vez generado el AFND solo necesitamos comprobar la equivalencia en el menú “Test” -> “Compare Equivalence” que nos dirá que son equivalentes, en este caso son equivalentes

03/09/2009

Expresiones Regulares con MySQL

Elementos

Operativa

Para interactuar con el sistema se envían las consultas sql al analizador de consultas este separa la consulta en parte y analiza la expresión regular

Sintaxis:

Tipo de Operador	Ejemplos	Descripción
Caracteres Literales. Coincidencia exacta	a A y 6 % @	Caracteres, Digitos y algunos caracteres especiales que coincidan exactamente
	\$ \^ \+ \\ \?	Precedencia de un carácter especial con \ para cancelar su significado como expresion regular
	\n \t \r	Nueva linea, tabulador o enter
	\cJ \cG	Codigos de Control
	\xa3	Codigos hexadecimales para cualquier carácter.
Anclajes	^	El campo empieza por
	$	El campo acaba por
	[[:<:]]	La palabra empieza por
	[[:>:]]	La palabra acaba por
Grupos de caracteres, cualquier carácter del grupo	[aAeEiou]	Cualquier carácter contenido en []
	[^aAeEiou]	Cualquier carácter excepto los contenidos en []
	[a-fA-F0-9]	Cualquier carácter hexadecimal (0 a 9 o a hasta f)
	.	Cualquier caracter
	[[:space:]]	Cualquier carácter separador (espacio \n \r o \t)
	[[:alnum:]]	Cualquier carácter alfanumerico
Contadores, actuan sobre elementos previos	+	1 o mas
	*	0 o mas
	?	0 o 1
	{4}	Exactamente 4
	{4,}	4 o mas
	{4,8}	Entre 4 y 8
	Añadir una ? Después de cualquier contador para convertirlo
Alternación	\|	o
Agrupamiento	()	Grupo para contar y guardar la variable

Ejemplos:

Actores cuyo nombre acabe por la letra A

SELECT * FROM actor where first_name REGEXP ‘A$’

Actores que hayan participado en peliculas de animación

SELECT * FROM actor_info where film_info REGEXP ‘Animation:’

Actores que hayan participado en peliculas de animación pero no en peliculas de Accion

SELECT * FROM actor_info where film_info REGEXP ‘Animation: ‘ and not film_info REGEXP ‘Action:’

Todas las peliculas que tengan escenas eliminadas

SELECT * FROM film where special_features regexp ‘Deleted Scenes’ and not special_features regexp ‘trailers’

Todas las direcciones que sean Lane

SELECT * FROM address where address regexp ‘lane’

Todos los alquileres del mes 5 del 2005

SELECT * FROM rental r where rental_date regexp ‘^2005-05’ order by rental_date ASC

Actores cuyo nombre tenga dos vocales seguidas

SELECT * FROM actor a where first_name regexp ‘((a|e|i|o|u){2})’

Fuentes

http://www.wellho.net/regex/mysql.html