universidade – La Fabulosa Vida de un IT

27/09/2011

Contraste de Hipótesis

Otro boletín a manita (mi letra sigue sin mejorar) 🙁

Boletín métodos estadísticos

Enjoy

27/09/2011

Distribución en el muestreo y Estimación Puntual

El ultimo boletin con mi letra, en este mundo existen cosas que no tienen arreglo y una de ella es mi letra 🙁

Boletín Distribución en el muestreo y Estimación Puntual

27/09/2011

Examen diciembre 2010 Métodos Estadísticos

1) (1,5 puntos) Dada una muestra aleatoria ${x_1,x_2, ..., x_100}$ de una distribución normal de media 16 y varianza 4, calcular el valor b tal que

2) (1,5 puntos) Encontrar el estimador máximo verosímil para el parámetro de la función de densidad:

3)(2 Puntos) El tiempo de acceso (en milisegundos) en situarse una aguja lectora/escritora en un cilindro se supone que sigue una distribución normal. Para determinar en el tiempo medio de acceso se obtuvo una muestra aleatoria de tamaño n=10, con , cuasivarianza muestral 1,75 .

Obtener un intervalo de confianza al 75% para , tiempo medio de acceso. A partir del intervalo anterior obtener el I.C. Para el tiempo medio en segundos.
¿Puedo asegurar en cualquier caso que el tiempo medio de acceso está siempre dentro del intervalo. Justifica tu respuesta
Observando el intervalo, ¿Puedo afirmar que el tiempo medio de acceso es 12ms? Justifica tu respuesta
Si se mantiene la media y cuasivarianza muestral al aumentar el tamaño muestral ¿Que le ocurre a la longitud del intervalo y a su nivel de confianza? Justifica tu respuesta..

4)(2 puntos) Según el informe del observatorio galego da sociedade da informacion del 2009, el porcentaje de hogares que disponen de conexión de banda ancha a internet es del 38,3% obtenida a partir de una muestra de 1000 hogares En 2008, una muestra de 1200 hogares indico que el 35,3% de los hogares disponían de banda ancha.

¿Se justifica la conclusión de que en 2008 hay un porcentaje distinto al 2009 con un nivel de significación del 5%? Responder sin usar el p-valor y calculando en p-valor.
Si los datos anteriores se mantuviesen constantes el aumentar los tamaños muestrales, como afectaría esta cambio a la decisión del contraste y al valor numérico del p-valor. Justifica tu respuesta.

enjoy

24/01/2011

Examen Diciembre 2008 Teoría

La información de carácter habitualmente reservado, que se elabora en el seno de una unidad económica, con el fin de conocer hechos o adoptar medidas que afecten a la gestión interna de aquellas se denomina:

Unidades de consumo
Unidades de producción
Información interna o de gestión
Información externa o financiera

Como clasificarías a un “consumidor” dentro de los posibles usuarios de la información contable

Usuarios vinculados de manera permanente a la empresa.
Usuarios externos pero relacionados con la empresa.
Usuarios externos sin relación con la empresa.
Usuarios institucionales que operan en el mercado de trabajo.

Según el Marco Conceptual del Plan general de Contabilidad, cual de esas condiciones debe ser cumplida por los pasivos para ser considerados como tales:

Debe estar controlado por la empresa.
Debe constituir una deuda presente.
Debe estar referido a sucesos pasados.
Opciones b) y c) son correctas.
Opciones a) y b) son correctas.

El activo representa:

Lo que la empresa debe al sujeto jurídico que aporto su capital.
Los bienes y derechos a favor de la empresa.
Las inversiones y fuentes financieras de la empresa.
El capital de la empresa.

Qué masa patrimonial representa la estructura económica o la inversión de la empresa:

Activo
Pasivo
Neto
Fondos Propios

Según el convenio de Cargo y Abono, señale donde se hace la anotación de:

Los libros contables, una vez aprobados se depositaran en el …

Registro Civil
Registro de la propiedad
Registro Mercantil
Autoridad Laboral Competente

Que significa que una cuenta tenga saldo deudor:

Que las anotaciones de debe son mayores que las de haber
Que las anotaciones de debe son menores que las de haber
Que las anotaciones del debe y el haber son las mismas
Que se trata de una cuenta de activo que recoge bienes o derechos y nace siempre por el debe

Con que frecuencia se ha de elaborar el balance de sumas y saldos:

Diariamente
Máximo mensual
Mínimo trimestral
Mínimo anual

El Plan general utiliza los grupos del 1 al 5 para conformar

El balance de saldos
El balance de situación
El balance de sumas y saldos
La cuenta de pérdidas y ganancias

El valor contable de un bien amortizable es:

El importe por el que el bien aparece reflejado en la cuenta representativa del mismo
La diferencia entre el saldo de la cuenta que o representa y su valor residual
El valor de compra del bien
La diferencia entre el saldo de la cuenta que lo representa y su amortización acumulada

La cuenta 610- Variación de existencias de mercaderías

Tendrá siempre un saldo deudor.
Tendrá siempre un saldo acreedor
Puede tener un saldo deudor, acreedor o nulo
No puede tener saldo nulo, pues la empresa siempre tiene que tener existencias

Uno de los criterios que se utilizan para saber que empresas puede aplicar el PGCPYMES es el volumen e cifra de negocios ¿Cual es la cuantiá que no se puede superar?

2.850.000
5.700.000
2.000.000
19.000.000

Las cuentas de activo figuraran siempre en el debe de los asientos

Verdadero
Falso

El método de la partida doble consiste en hacer una doble anotación

Verdadero
Falso

Enjoy

11/06/201002/09/2010

Consultas Laboratorio BD

Transparencias Teoría de Prácticas– SQL como DML 2010

EJERCICIOS

Los corregidos están en azul:

– Nombre de los empleados que trabajan en el departamento 121

[SQL]

SELECT Nomem

FROM Temple

WHERE numde=121

[/SQL]

– Extraer todos los datos del departamento 121

SELECT *

FROM tdepto

WHERE numde=121

– Obtener los nombres y sueldos de los empleados con más de 3 hijos por orden alfabetico

SELECT Nomem, salar

FROM Temple W

HERE numhi>3

ORDER BY Nomem

– Obtener la comisión, departamentos y nombre de los empleados cuyo salario es inferior a 1900 euros, clasificándolos por departamento en orden creciente, y por comisión en orden decreciente dentro de cada departamento.

SELECT comis, numde, Nomem

FROM Temple

WHERE salar<1900

ORDER BY numde, comis desc;

– Igual que la anterior, pero las columnas resultantes han de llamarse comision, depto y empleado

SELECT comis as comision, numde as depto, Nomem as empleado

FROM Temple

WHERE salar<1900

ORDER BY numde, comis desc;

– Números de los departamentos donde trabajan empleados con salario inferior a 2500

SELECT numde

FROM Temple

WHERE salar<2500

– Obtener los valores diferentes de comisiones que hay en el departamento 110

SELECT distinct comis

FROM Temple

WHERE numde=110

– Hallar las combinaciones diferentes de valores de salario y comision en el departamento 111, por orden de salario y comisión crecientes.

SELECT distinct salar, comis

FROM Temple

WHERE numde=111

ORDER BY salar,comis

-Obtener los nombres de los emleados cuya comision es superior o igual al 50% de su salario, por orden alfabético

SELECT Nomem

FROM Temple

WHERE comis>=(salar/2)

ORDER BY 1

-Obtener por orden alfabético los nombres de los empleados cuyo salario supera al máximo salario de los empleados del departamento 123.

SELECT Nomem

FROM Temple

WHERE salar> all(SELECT salar FROM Temple WHERE numde=’123′)

ORDER BY 1;

-Obtener por orden alfabético los nombres de los empleados cuyo sueldo supera en tres veces y media o más al mínimo salario de los empleados del departamento 122

SELECT Nomem

FROM Temple

WHERE salar/3.5> some (SELECT salar FROM Temple WHERE numde=’122′)

ORDER BY 1;

EJERCICIOS PREDICADOS

1- Para todos los empleados que tienen Comisión, hallar sus Salarios mensuales totales incluyendo ésta. Ordenarlos por orden alfabético. Hallar también el porcentaje de su Salario total que supone la Comisión.

SELECT Nomem, (Salar + Comis)*12 as Salario_total, Salar/Comis as porcentaje

FROM Temple

WHERE Comis is not null and Comis<>0

ORDER BY Nomem;

2- Mostrar nombres y presupuestos de los departamentos 111 y 112, de tal manera que aparezcan en la misma fila.

SELECT uno.Nomde, uno.Presu, dos.Nomde, dos.Presu

FROM Tdepto uno, Tdepto dos

WHERE uno.Numde=’111′ and dos.Numde=’112’;

3- Obtener los nombres de los departamentos que no dependen funcionalmente de otros.

SELECT Numde

FROM Tdepto

WHERE depde is null;

4- Para los empleados que no tienen Comisión obtener por orden alfabético el nombre y el cociente entre su Salario y el número de hijos.

SELECT Nomem, Salar/Numhi as cociente

FROM Temple

WHERE (Comis is null or Comis=0) and Numhi>0

ORDER BY 1;

5- Obtener por orden alfabético los nombres de los empleados cuyo Salario supera al máximo Salario de los empleados del departamento 122.

SELECT Nomem

FROM Temple

WHERE Salar> all (SELECT Salar FROM Temple WHERE Numde=122)

ORDER BY 1;

6- Obtener por orden alfabético los nombres de los empleados cuyo Salario supera en tres veces y media o más al mínimo Salario de los empleados del departamento 122.

SELECT Nomem

FROM Temple

WHERE Salar>= some (SELECT Salar*3.5 FROM Temple WHERE Numde=122)

ORDER BY 1;

7- Obtener por orden alfabético los nombres de los empleados cuyo Salario supera en tres veces y media o más al mínimo Salario de los empleados del departamento 123. Razonar el resultado.

SELECT Nomem

FROM Temple

WHERE Salar/3.5>= some (SELECT Salar FROM Temple WHERE Numde=123)

ORDER BY 1;

No sale ninguna fila porque el departamento 123 no existe.

8- Obtener los nombres y Salarios de los empleados cuyo Salario coincide con la Comisión de algún otro o la suya propia. Ordenarlos alfabéticamente.

SELECT unique t.Nomem,t.Salar

FROM Temple t, Temple td

WHERE t.Salar=td.Comis

ORDER BY 1;

9- Obtener por orden alfabético los nombres y Salarios de los empleados cuyo Salario es inferior a la Comisión más alta existente.

SELECT Nomem,Salar

FROM Temple

WHERE Salar< (SELECT max(Comis) FROM Temple)

ORDER BY 1;

SELECT Nomem,Salar

FROM Temple

WHERE Salar< all(SELECT Comis FROM Temple)

ORDER BY 1;

10- Obtener por orden alfabético los nombres y Salarios de los empleados cuyo Salario es inferior al cuádruplo de la Comisión más baja existente.

SELECT Nomem,Salar

FROM Temple

WHERE Salar<4*(SELECT min(Comis) FROM Temple)

ORDER BY 1,2;

SELECT Nomem,Salar

FROM Temple

WHERE Salar< some(SELECT Comis*4 FROM Temple)

ORDER BY 1,2;

11- Obtener por orden alfabético los nombres de los empleados cuyo Salario está entre 2500 y 3000 euros.

SELECT Nomem,Salar

FROM Temple

WHERE Salar between 2500 and 3000

ORDER BY 1,2;

12- Obtener por orden alfabético los nombres y los Salarios de los empleados cuyo Salario dividido por su número de hijos cumpla una, o ambas, de las dos condiciones siguientes

a) Que sea inferior a 1200 euros

b) Que sea superior al doble de su Comisión Ejercicio de examen

SELECT Nomem,Salar

FROM Temple

WHERE (((Salar/Numhi<1200) or ((Salar/Numhi)>(2*Comis))) and Numhi>0

ORDER BY 1;

13- En la fiesta de Reyes se desea organizar un espectáculo para los hijos de los empleados, que se representará en dos días diferentes. El primer día asistirán los empleados cuyo apellido empiece por las letras desde A hasta L, ambas inclusive. El segundo día se cursarán invitaciones para el resto. A cada empleado se le asignarán tantas invitaciones gratuitas como hijos tenga y dos más. Además en la fiesta se entregará a cada empleado un obsequio por hijo. Obtener una lista por orden alfabético de los nombres a quienes hay que invitar el primer día de la representación, incluyendo también cuántas invitaciones corresponden a cada nombre y cuántos regalos hay que preparar para él. (Obsérvese que si dos empleados están casados, esta consulta calculará dos veces el número de invitaciones familiar si los hijos figuran en la tabla tanto en la fila del marido como de la esposa).

SELECT Nomem,Numhi+2 as invitaciones, Numhi as obsequios

FROM Temple

WHERE Nomem between ‘A%’ and ‘M%’;

14- Obtener por orden alfabético los nombres de los empleados cuyo primer apellido es Mora o empieza por Mora

SELECT Nomem

FROM Temple

WHERE Nomem like ‘MORA%’

ORDER BY 1;

15- Obtener por orden alfabético los nombres de los empleados cuyo nombre de pila empieza por Valeriana.

SELECT Nomem

FROM Temple

WHERE Nomem like ‘%, VALERIANA%’

ORDER BY 1;

16- Obtener por orden alfabético los nombres de los empleados cuyo apellido tenga siete letras.

SELECT Nomem

FROM Temple

WHERE Nomem like ‘_ _ _ _ _ _ _,%’;

17- Obtener por orden alfabético los nombres de los empleados cuyo apellido tenga seis o más letras.

SELECT Nomem

FROM Temple

WHERE Nomem like ‘_ _ _ _ _ _%,%’;

18- Obtener los nombres de los empleados cuyo apellido tenga tres letras o menos.

SELECT Nomem

FROM Temple

WHERE Nomem not like ‘_ _ _ _%,%’;

19- Obtener por orden alfabético los nombres de los empleados cuyo apellido termina en EZ y su nombre de pila termina en O y tiene al menos tres letras.

SELECT Nomem

FROM Temple

WHERE Nomem like ‘%EZ, _ _O’ ORDER BY 1;

20- Se desea hacer un regalo de un 1 % del Salario a los empleados en el día de su onomástica. Hallar por orden alfabético los nombres y cuantía de los regalos en euros para los que celebren su santo el día de San Honorio.

SELECT Nomem, Salar, Salar*0.01 as regalo

FROM Temple

WHERE Nomem like ‘%, %HONORI_ %’ (Para José Honorio De Todos los Santos)

ORDER BY 1;

21- Obtener por orden alfabético los nombres de los empelados que trabajan en el mismo departamento que Pilar Gálvez o Dorotea Flor

SELECT Nomem, Numde

FROM Temple

WHERE Numde in (SELECT Numde FROM Temple WHERE Nomem like ‘GALVEZ, PILAR’ or Nomem like ‘FLOR, DOROTEA’)

ORDER BY 1;

SELECT Nomem, Numde

FROM Temple

WHERE Numde in (SELECT Numde FROM Temple WHERE Nomem in (‘GALVEZ, PILAR’, ‘FLOR, DOROTEA’))

ORDER BY 1;

SELECT Nomem, Numde

FROM Temple

WHERE Numde = SOME (SELECT Numde FROM Temple WHERE Nomem in (‘GALVEZ, PILAR’, ‘FLOR, DOROTEA’))

ORDER BY 1;

(“IN” es igual o equivalente a “ = SOME”)

22- Obtener una lista por orden alfabético de los empleados cuyo Salario coincida con el de alguno de los empleados del departamento 100. Resolver de dos maneras diferentes.

a) SELECT Nomem, Numde, Salar

FROM Temple

WHERE Salar IN (SELECT Salar FROM Temple WHERE Numde=100)

ORDER BY 1;

b) SELECT Nomem, Numde, Salar

FROM Temple

WHERE Salar = SOME (SELECT Salar FROM Temple WHERE Numde=100)

ORDER BY 1;

23- Obtener los nombres de los centros de trabajo si hay alguno que esté en la calle Atocha.

SELECT nomce, señas

FROM Tcentr

WHERE exists (SELECT nomce FROM Tcentr WHERE señas like ‘%ATOCHA%’);

24- Obtener por orden alfabético los nombres y Salarios de los empleados del departamento 111 que tienen Comisión si hay alguno de ellos cuya Comisión supere al 15 % de su Salario.

SELECT Nomem, Salar

FROM Temple

WHERE Numde=111 and Comis is not null and exists

(SELECT Comis FROM Temple WHERE Comis>Salar*0.15 and Numde= 111 and Comis is not null)

ORDER BY 1;

25- Obtener por orden alfabético los nombres y Comisiones de los empleados del departamento 110 si hay en él algún empleado que tenga Comisión.

SELECT Nomem, Comis

FROM Temple

WHERE Numde=110 and exists (SELECT * FROM Temple WHERE Comis<>0 or Comis<>null) ORDER BY 1;

26- Obtener los nombres, Salarios y fechas de ingreso de los empleados que, o bien ingresaron después de 1.1.88, bien tienen un Salario inferior a 2000 euros. Clasificarlos por fecha y nombre.

SELECT Nomem, Salar,fecin

FROM Temple

WHERE fecin >’1.1.88′ or Salar <2000

ORDER BY 3, 1;

27 – Obtener por orden alfabético los nombres de los departamentos que no sean de Dirección ni de Sectores.

SELECT Nomde

FROM Tdepto

WHERE Nomde<>’Direccion’ and Nomde<>’Sectores’

ORDER BY 1;

28- Obtener por orden alfabético los nombres y Salarios de los empleados que o bien no tienen hijos y ganan más de 2000 euros, o bien tienen hijos y ganan menos de 3000 euros.

SELECT Nomem,Salar

FROM Temple

WHERE (Numhi=0 and Salar>2000) or

(Numhi<>0 and Salar<3000)

ORDER BY 1;

SELECT Nomem,Salar

FROM Temple

WHERE (Numhi is null and Salar>2000) or

(Numhi is not null and Salar<3000)

ORDER BY 1;

29- Hallar por orden alfabético los nombres y Salarios de empleados de los departamentos 110 y 111 que o bien no tengan hijos o bien su Salario por hijo supere a 1000 euros, si hay alguno sin Comisión en los departamentos 111 ó 112.

SELECT Nomem, Salar

FROM Temple

WHERE (Numde= 110 or Numde= 111) and (Numhi = 0 or (Salar/Numhi) <1000) and exists (SELECT 1 FROM Temple WHERE Comis is null and Numde IN (111, 112))

ORDER BY 1;

30- Hallar por orden alfabético los nombres de departamentos que o bien tienen directores en funciones o bien en propiedad y su Presupuesto anual excede a 50.000 euros o bien no dependen de ningún otro.

SELECT Nomde

FROM Tdepto

WHERE tidir=’P’ or tidir=’F’ and (Presu >50000 or depde is null)

ORDER BY 1;

EJERCICIOS DE AGREGACION Y AGRUPAMIENTO

1- Hallar el salario máximo para el conjunto de empleados del departamento 100.

SELECT max(salar)

FROM Temple

WHERE numde=100;

2- Obtener por orden alfabético los salarios y nombres de los empleados cuyo salario se diferencia con el máximo en menos de un 40% de éste.

SELECT numem, salar

FROM Temple

WHERE salar>0.6*(SELECT max(salar) FROM Temple));

3- Hallar el número de empleados de la empresa.

SELECT count(*)

FROM Temple;

4- Hallar el número de empleados y de extensiones telefónicas del departamento 112.

SELECT count (*) as numero_de_empleados, count(distinct extel) as

extensiones_telefonicas

FROM Temple

WHERE numde=112;

5- Hallar el número de empleados del departamento 112, así como cuántas comisiones hay y la suma y media de sus comisiones.

SELECT count(*) as numero_de_empleados, count(comis) as comisiones,

avg(comis) as media_comisiones, sum(comis) as suma_comisiones

FROM Temple

WHERE numde=112;

6- Hallar cuántas comisiones diferentes hay y su valor medio.

SELECT count (distinct comis),avg(comis)

FROM Temple;

7- Hallar la media del número de hijos de los empleados del departamento 123.

SELECT count(*)

FROM Temple

WHERE fecna<’01/01/29′;

8- Hallar para cada departamento que depende del 100 su número y su presupuesto, junto con la media del presupuesto de todos los departamentos.

SELECT numde,presu,(SELECT avg(presu) FROM tdepto)

FROM tdepto

WHERE depde=100;

9 – Obtener por orden alfabético los nombres de los empleados cuyo salario supera en tres veces y media o más al mínimo salario de los empleados del departamento 123. Razonar el resultado.

Utilizar funciones de agregación y agrupación.

Select nomem

From temple

Where salar > 3.5 *(select min (salar) from temple where numde=123)

Order by 1;

10- Hallar cuántos departamentos hay y el presupuesto anual medio de ellos.

SELECT count(*),avg(presu)

FROM tdepto

11- Como la pregunta anterior, pero para los departamentos que no tienen director en

propiedad.

SELECT count(*),avg(presu)

FROM tdepto

WHERE tidir<>’P’;

12- Hallar por orden de número de empleado el nombre y salario total (salario más comisión) de los empleados cuyo salario total supera al salario mínimo en 3000 euros mensuales.

SELECT numem,Nomem, salar+nvl(comis,0)

FROM Temple

WHERE ((salar+nvl(comis,0))-(SELECT min(salar) FROM Temple))>3000

ORDER BY numem;

De años anteriores

10- Resolver el ejercicio 7 del boletín de predicados utilizando funciones de agregación.

SELECT Nomem

FROM Temple

WHERE salar>= 3.5*(SELECT min(salar) FROM Temple WHERE numde=123)

ORDER BY 1;

11- Resolver el ejercicio 9 del boletín de predicados utilizando funciones de agregación.

SELECT Nomem,salar

FROM Temple

WHERE salar<(SELECT max(comis) FROM Temple)

ORDER BY 1;

12- Resolver el ejercicio 10 del boletín de predicados utilizando funciones de agregación.

SELECT Nomem,salar

FROM Temple

WHERE salar> 4*(SELECT min(comis) FROM Temple)

ORDER BY 1;

13- Hallar la masa salarial anual (salario más comisión) de la empresa (se suponen 14 pagas anuales).

SELECT (sum(salar)+sum(comis))*14 as masa_salarial_anual

FROM Temple;

Esto está mal porque los valores nulos de comis no los cuenta.

Correcto:

SELECT sum(salar + nvl(comis,0))*14

FROM Temple;

Nvl (arg1,arg2) -> Si arg1 distinto de nulo devuelve arg1. Si arg1 igual a nulo devuelve arg2.

14- Hallar el salario medio de los empleados cuyo salario no supera en más de 20 % al salario mínimo de los empleados que tienen algún hijo y su salario medio por hijo es mayor que 1000 euros.

SELECT avg(salar)

FROM Temple

WHERE salar<1.2*(SELECT min(salar) FROM Temple WHERE numhi<>0 and (salar/numhi)>1000);

15- Hallar la diferencia entre el salario más alto y el más bajo.

SELECT max(salar)-min(salar) as diferencia

FROM Temple;

16- Hallar el presupuesto medio de los departamentos cuyo presupuesto supera al presupuesto medio de los departamentos.

SELECT avg(presu)

FROM tdepto

WHERE presu >(SELECT avg(presu) FROM tdepto);

17- Hallar el número medio de hijos por empleado para todos los empleados que no tienen más de dos hijos.

SELECT avg(numhi)

FROM Temple

WHERE numhi<3

18- Hallar el número de empleados de los departamentos 100 y 110.

SELECT count(NUMDE),numde

FROM Temple

WHERE numde in(100,110)

group BY numde;

19- Agrupando por departamento y número de hijos, hallar cuántos empleados hay en cada grupo para los departamentos 100 y 110.

SELECT count(*),numde, numhi

FROM Temple

WHERE numde in(100,110)

group BY numde, numhi

ORDER BY numhi;

20- Para los departamentos en los que hay algún empleado cuyo salario sea mayor que 4000 euros al mes hallar el número de empleados y la suma de sus salarios, comisiones y número de hijos.

SELECT count(numem),sum(salar),sum(comis),sum(numhi),numde

FROM Temple

group BY numde having numde in(SELECT distinct (numde) FROM Temple WHERE salar>4000);

21- Agrupando por número de hijos, hallar la media por hijo del salario total (salario y comisión).

SELECT numhi, sum((salar+nvl(comis,0))/numhi)

FROM Temple

WHERE numhi>0

group BY numhi

ORDER BY 1

24- Para cada departamento, hallar la media de la comisión con respecto a los empleados que la reciben y con respecto al total de empleados.

SELECT numde, avg(comis), sum(comis)/cont(*) as mediatotal

FROM Temple

WHERE comis is not null

group BY numde

23- Para cada extensión telefónica hallar cuántos empleados la usan y el salario medio de éstos.

SELECT count(numem),avg(salar),extel

FROM Temple

group BY extel

ORDER BY extel ;

24- Para cada extensión telefónica y cada departamento hallar cuántos empleados la usan y el salario medio de éstos.

SELECT count(numem),avg(salar),extel,numde

FROM Temple

group BY extel,numde

ORDER BY extel;

25- Hallar los números de extensión telefónica mayores de los diversos departamentos, sin incluir los números de éstos.

SELECT max(extel)

FROM Temple

group BY numde

ORDER BY 1;

26- Para cada extensión telefónica hallar el número de departamentos a los que sirve.

SELECT extel,count(numde)

FROM Temple

group BY extel

ORDER BY 1;

27- Para los departamentos en los que algún empleado tiene comisión, hallar cuántos empleados hay en promedio por cada extensión telefónica.

SELECT numde,count(*)/count(distinct extel)

FROM Temple

Where numde in (SELECT distinct (numde) FROM Temple WHERE comis is not null)

Group by numde;

Hacerlo conhaving!!!!

28- Para los empleados que tienen comisión, hallar para los departamentos cuántos empleados hay en promedio por cada extensión telefónica.

SELECT numde,count(*)/count(distinct extel)

FROM Temple

WHERE comis is not null

group BY numde;

29- Hallar los departamentos que tienen más de 2 extensiones teléfónicas.

SELECT numde, count(distinct(extel))

FROM Temple

group BY numde

having count (distinct(extel)) > 2

30- Hallar los departamentos cuyo salario medio es mayor a 1500

SELECT numde,

FROM Temple

group BY numde

having avg(salar)> 1500

31- Hallar los departamentos cuyo valor mayor de extensión telefónica es superior a 150.

SELECT numde,

FROM Temple

group BY numde

having MAX(extel) > 150

Si pudieramos una select subordinada escalar having(Select max extel from temple)>150 lo que hariamos es coger las extensiones mayores de toda la tabla temple. En la primera esta agrupado por grupos.

Correlacionada:

SELECT numde,

FROM Temple

group BY numde

having MAX(extel) > 150

32- Para los departamentos cuyo salario medio supera al de la empresa, hallar cuántas extensiones telefónicas tienen.

SELECT numde, count(distinct extel)

FROM Temple

group BY numde having avg(salar)>(SELECT avg(salar) FROM Temple);

33- Para cada centro hallar los presupuestos medios de los departamentos dirigidos en propiedad y en funciones, excluyendo del resultado el número del centro.

SELECT avg(presu),tidir

FROM tdepto

group BY numce,tidir;

34- Obtener por orden creciente los números de extensiones telefónicas de los departamentos que tienen más de dos y que son compartidas por menos de 4 empleados, excluyendo las que no son compartidas.

Solución 1:

SELECT extel

FROM Temple

WHERE numde in (SELECT numde FROM Temple group BY numde having count (distinct extel) > 2)

GROUP BY extel

having count (numem) BETWEEN 2 AND 3

ORDER BY 1;

Solución 2:

SELECT extel

FROM Temple

WHERE numde in (SELECT numde FROM Temple group BY numde having count (distinct extel) > 2) and extel in (SELECT extel FROM Temple group BY extel having count (numem) < 4 and count(numem)>1)

ORDER BY 1;

Solución 3:

SELECT extel

FROM Temple

group BY extel

WHERE numde in(SELECT numde FROM Temple group BY numde having count(distinct extel) > 2) having count(*)> 1 and count (*) < 4

ORDER BY 1;

35- Hallar el máximo valor de la suma de los salarios de los departamentos.

SELECT sum(salar),numde

FROM Temple

group BY numde

having sum(salar)>=all(SELECT sum(salar)FROM Temple group BY numde);

EJERCICIOS CONSULTAS SOBRE VARIAS TABLAS

1- Averiguar los nombres de los departamentos que tienen un presupuesto inferior a 100.000 euros, así como el nombre del centro de trabajo donde se encuentran ubicados.

SELECT Nomde, c.nomce, presu

FROM tcentr c, tdepto d

WHERE c.numce=d.numce and d.presu<100000

ORDER BY 3;

2- Hallar el salario máximo para el conjunto de empleados del departamento FINANZAS.

SELECT max(e.salar)

FROM Temple e, tdepto d

WHERE d.Nomde=’FINANZAS’ and e.numde=d.numde;

3- Obtener por orden alfabético los salarios, número de empleado y nombre de departamento de los empleados cuyo salario se diferencia con el máximo en menos de un 40% de éste.

SELECT numem, salar,d.Nomde

FROM Temple e,tdepto d

WHERE salar>0.6*(SELECT max(salar) FROM Temple) and d.numde=e.numde;

4- Hallar el número de empleados y de extensiones telefónicas del departamento PERSONAL.

SELECT count(*), count(distinct extel)

FROM Temple e, tdepto d

WHERE e.numde=d.numde and d.Nomde=’PERSONAL’;

5- Hallar el número de empleados del departamento PERSONAL, así como cuántas comisiones hay y la suma y media de sus comisiones.

SELECT count(e.numem),count(e.comis),sum(e.comis),avg(e.comis)

FROM Temple e, tdepto d

WHERE e.numde=d.numde and d.Nomde=’PERSONAL’;

6- Hallar la media del número de hijos de los empleados del departamento PROCESO DE DATOS.

SELECT avg(numhi)

FROM Temple e, tdepto d

WHERE e.numde=d.numde and Nomde=’PROCESO DE DATOS’;

7- Hallar para cada departamento que depende del depto DIRECC. COMERCIAL su número y su presupuesto, junto con la media del presupuesto de todos los departamentos.

SELECT t1.numde,t1.presu, (SELECT avg(presu) FROM tdepto)

FROM tdepto t1, tdepto t2

WHERE t1.depde=t2.numde and t2.Nomde=’DIRECC. COMERCIAL’

8- Hallar por orden de número de empleado el nombre del departamento, nombre del empleado y salario total (salario más comisión) de los empleados cuyo salario total supera al salario mínimo en 1000 euros mensuales.

SELECT Nomde,numem,Nomem, salar+nvl(comis,0)

FROM Temple e, tdepto d

WHERE e.numde=d.numde and (salar+nvl(comis,0))>(SELECT min(salar) FROM Temple)+1000 ORDER BY numem;

9- Si el departamento 122 está ubicado en la calle Alcalá, obtener por orden alfabético los nombres de aquellos empleados cuyo salario supere al salario medio de su departamento.

SELECT e.Nomem

FROM Temple e

WHERE e.salar>(SELECT avg(salar)FROM Temple e2 WHERE e2.numde=e.numde) and exists(SELECT * FROM tdepto d, tcentr c WHERE d.numde=122 and c.señas like ‘%ALCALA%’ and d.numce=c.numce);

Para cada departamento con presupuesto inferior a 60.000 euros, hallar el nombre del centro donde está ubicado y el máximo salario de sus empleados, si éste excede a 2000 euros. Clasificar alfabéticamente por nombre de departamento.

Solucion 1:

SELECT d.Nomde,c.nomce,max(salar)

FROM Temple e, tdepto d, tcentr c

WHERE d.numce=c.numce and e.numde=d.numde and presu<60000

group BY d.Nomde,c.nomce having max(e.salar)>2000;

11- Hallar por orden alfabético los nombres de los departamentos que dependen de los que tienen un presupuesto inferior a 50.000 euros.

SELECT t1.Nomde

FROM tdepto t1, tdepto t2

WHERE t1.depde=t2.numde and 2.presu<50000

ORDER BY 1;

12- Para los departamentos cuyo presupuesto anual supera a 60 000 euros, hallar cuántos empleados hay en promedio por cada extensión telefónica.

Solucion1:

SELECT count(numem)/count(distinct extel),d.Nomde

FROM Temple e, tdepto d

WHERE e.numde=d.numde and d.presu>60000

group BY d.Nomde;

Solucion2:

SELECT count(numem)/count(distinct extel

FROM Temple

WHERE numde in (Select numde from tdepto where presu>60000)

group BY Nomde;

Solucion3:

SELECT count(numem)/count(distinct extel

FROM Temple

WHERE Exist (Select 1 from tdepto where tdepto.numde= temple.numde and presu>60000)

group BY Nomde;

13- Obtener por orden alfabético los nombres de empleados cuyo apellido empieza por G y trabajan en un departamento ubicado en algún centro de trabajo de la calle Alcalá.

SELECT e,Nomem

FROM Temple e,tdepto d,tcentr c

WHERE e.numde=d.numde and d.numce=c.numce and e.Nomem like ‘G%’ and c.señas like ‘%ALCALA%’;

14- Hallar por orden alfabético los distintos nombres de los empleados que son directores en funciones.

Solucion 1:

SELECT Nomem

FROM Temple e,tdepto d

WHERE e.numem=d.direc and d.tidir=’F’

ORDER BY 1;

Solucion 2:

SELECT Nomem

FROM Temple

WHERE numem in (select direc from tdepto where tdir= ‘F’)

ORDER BY 1;

15- Para todos los departamentos que no sean de dirección ni de sectores, hallar número de departamento y sus extensiones telefónicas, por orden creciente de departamento y, dentro de éste, por número de extensión creciente.

SELECT d.numde,e.extel

FROM tdepto d, Temple e

WHERE e.numde=d.numde and d.Nomde not like ‘%SECTOR%’ and d.Nomde not like ‘%DIRECCION%’

ORDER BY 1,2;

16- A los distintos empleados que son directores en funciones se les asignará una gratificación del 5 % de su salario. Hallar por orden alfabético los nombres de estos empleados y la gratificación correspondiente a cada uno.

SELECT e.Nomem,(e.salar*1.05) as gratificacion

FROM Temple e, tdepto d

WHERE e.numem=d.direc and d.tidir=’F’

ORDER BY 1;

17- Hallar por orden alfabético los nombres de los empleados cuyo director de departamento es Marcos Pérez, bien en propiedad o bien en funciones, indicando cuál es el caso para cada uno de ellos.

SELECT distinct(e.Nomem) ,(SELECT d2.tidir FROM tdepto d2 WHERE d2.numde=e.numde) as tipo

FROM Temple e,tdepto d

WHERE e.numde=d.numde and d.direc= (SELECT numem FROM Temple WHERE Nomem like ‘PEREZ, MARCOS’)

ORDER BY 1;

18- Hallar por orden alfabético los nombres de los empleados que dirigen departamentos de los que dependen otros departamentos, indicando cuántos empleados hay en total en éstos.

SELECT e.Nomem

FROM Temple e, tdepto d

WHERE e.numde=d.numde and d.direc=e.numem and d.numde in (SELECT d1.numde FROM tdepto d1,tdepto d2 WHERE d2.depde=d1.numde )

ORDER BY 1;

07/06/2010

Examen informática gráfica septiembre 2006

Parte 1.-Preguntas Tipo Test

a.En el proceso de obtención de imágenes, el recortado se hace después de la proyección
- Falso, el recortado se hace antes(TEMA 1 pg:17)
b.La transformación del modelo supone un cambio en el sistema de coordenadas
- ¿Verdadero? (Porque cambian las coordenadas del objeto)
c.El proceso de visualización consiste en eliminar partes de los objetos que quedan ocultas al observador
- Falso(TEMA 4) Sumario.
d.La proyección es el paso de un sistema de coordenadas a otro de menor dimensión
- ¿Falso? Tema 4. Pg: 6
e.Si el escalado en el eje y es negativo, entonces el objeto se refleja respecto del eje x
- Verdadero. Tema 3. Pg:7
f.Las coordenadas homogéneas permiten tratar la traslación como el escalado y la rotación
- Verdadero. Tema 3. Pg:10
g.En el GCS existen múltiples representaciones para un mismo objeto
- ¿Falso? Tema 2. Pg 12
h.En una proyección de perspectiva, el tamaño de la proyección varia uniformemente con la distancia
- Falso. Disminuye de Tamaño de forma no uniforme. Tema 4. Pg:6
i.La proyección de perspectiva da realismo visual
- Verdadero. Tema 4. Pg:6
j.En la fase de modelado es necesario modelar todos los objetos de la escena de manera que siempre desarrollemos modelos de alta resolucion
- ¿Falso?
k.La representación con puntero a la lista de aristas es la única de las 3 representaciones donde cada vértice se almacena una unica vez
- Verdadero. Tema 2. Pg. 9
l.En el volumen de la vista para una proyección paralela ortográfica, los ángulos de la vista son cero
- Verdadero. Tema 4.Pg: 15
m.En el modelo de cámara sintética, la orientación es definida por los vectores LOOK y UP
- Verdadero. Tema 4.Pg: 11
n.En el algoritmo del pintor es necesario una ordenación previa de los objetos
- Verdadero. Tema 5. Pg:6
o.En el algoritmo ZBuffer, la memoria de profundidad debe inicializarse a la coordenada Z del plano de recorte delantero.
- Verdadero. Tema 5.Pg:4

2.Dado un cuadrado cuyos lados tienen una longitud de 4 unidades que se encuentra situado en el origen de coordenadas, obtener la matriz de transformación que hay que aplicar para que el vértice superior derecho estea situado en (8,10) y el vértice inferior izquierdo en el punto (6,4). ( 2,5 puntos )

T( 6 , 4 ) . S( 0.5 , 1.5 ) . T( 2 , 2 )

3¿ Cual es la condición para que el producto de matrices escalado-rotación sea uniforme ? ( 1 Punto )

¿?Que sean matrices cuadradas con el mismo numero de filas que de columnas.

4.Responde de forma muy breve: ( 1,5 Puntos )

a.Proceso de visibilidad
- ¿?El proceso consiste en: recortado contra el volumen de la vista, proyección sobre el plano de proyecciones y transformación al marco del dispositivo.
b.Transformación de la vista
- Visualización precisa de un observador. La transformación de la vista, una vez conocida la posición del observador, supone un cambio de coordenadas de la escena al sistema local de observación.
c.Transformación del dispositivo
- El cambio de sistema de coordenadas del mundo real (vista) al del dispositivo se conoce como transformación del dispositivo.

05/06/2010

Examen Informatica Grafica Junio 2006

Ejercicio 1: 21 Preguntas tipo test (Verdadero/ Falso)

En el proceso de obtención de imágenes, el recortado se hace, en general, después del proceso de proyección.
- Falso, se hace antes.
La transformación del modelo supone un cambio en el sistema de coordenadas
- ¿Verdadero? (Porque cambian las coordenadas del objeto)
El proceso de visibilidad consiste en eliminar partes de objetos ocultas al observador
- ?Verdadero¿
La proyección es el paso de un sistema de coordenadas a otro de menor dimensión
- Falso.
Si el escalado en x es negativo el objeto se refleja respecto del eje x.
- Falso, se refleja sobre el eje y.
Las coordenadas homogéneas permiten tratar la traslación como rotación y escalado.
- Verdadero
En la representación como punteros a la lista de aristas es fácil ver que aristas compartes vértices
- Falso.
En el modelado B-REP y CGS se usa la unión, intersección y diferencia para crear objetos
- Verdadero.
Al cambiar el vector UP los objetos aparecen rotados
- ¿Verdadero?
Si el vector UP es perpendicular al plano de proyección , entonces la proyección esta mal definida
- Falso.
Si el centro de proyecciones esta en el plano de proyección entonces la proyección esta mal definida
- Verdadero
El método del pintor es independiente de la resolución del dispositivo
- ¿Verdadero?
El algoritmo Warknot, se realiza hasta que todos los objetos son disjuntos, ya que tienen toda su influencia en elementos de interés.
- Verdadero.

EJERCICIO 2 : Decir que respuesta es la correcta, respecto a la traslación de los objetos A y B.

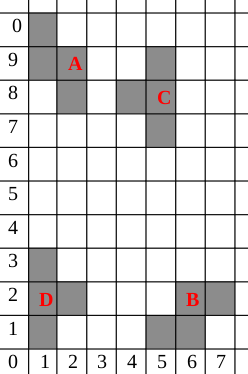a)A->B : T(0,-8) R(90) T(6,0)
C->D : T(-5,-9) R(-180)

b)A->B : R(-90) T(5,-7)
C->D : R(-180) T(-4,-6)

c)A->B : (T0,-10) R(-90) T(7,0)
C->D : T(-4,-6) R(180)

d)La a y la b.

e)ninguna

EJERCICIO 3 : Describir los poligonos según su lista de vértices.

Polígono P1 (V1,V3,V2) y P2(V2,V3, V5, V4).

28/05/201002/01/2015

Respuestas a las preguntas de teoría de los exámenes de TALF

Ahora que se acabaron las practicas y las hojas de talf lo único que queda son las respuestas a las preguntas de teoría y como no las tengo podíamos intentar completarlas entre todos (dejáis un comentario con la pregunta y la respuesta).

Ya están acabadas, gracias por vuestra nula colaboración

Exámen Xuño de 2005

Dado dos lenguajes regulares L1 y L2 . ¿El lenguaje de unión L1 ∪ L2 también es un lenguaje regular?

Cierto, porque L1 y L2 al ser regulares existe una expresión regular que los define cada lenguaje, dichas expresiones se pueden concatenar para generar el lenguaje que define la union.

¿Un autómata finito determinista siembre tiene un número mayor de estados que un autómata finito no–determinista asumiendo que ambos aceptan el mismo lenguaje?

Falso, sobre un autómata finito determinista podemos añadir transiciones epsilon a nuevos estados sin alterar el lenguaje que genera

¿L+ != L∗ si y solo si ∈ L?

Respuesta

¿Existen lenguajes libres de contexto que no son regulares?

Verdadero Un lenguaje libre de contexto es generado por una gramática libre de contexto y la gramática $ -> a$b | € genera el lenguaje no regular a^nb^n : N>=0

¿Si una gramática es ambigua también el lenguaje que genera es ambiguo?

No, para que un lenguaje sea ambiguo todas las gramáticas que lo generan tienen que ser ambiguas no es suficiente con una

¿Una gramática regular puede ser ambigua?

Si, por ejemplo
$ -> aA | aB
A->b
B->b (es regular y ambigua)

¿Existen expresiones regulares que definen lenguajes que no se pueden aceptar con un autómata finito con pila?

No porque para toda ER existe un AF y por definición todo AF es un AFP en el que la pila no se mueve

¿Un autómata finito con pila determinista puede realizar cambios de estados sin leer un símbolo de la entrada?

Si, siempre cuando realice una lectura y para esa lectura solo exista un camino

¿Si dos expresiones regulares no son iguales, los lenguajes que definen pueden ser iguales?

Si,

¿Para L = L(α) con α = a∗ b∗ c∗ , RL tiene índice 4?

Si, el autómata mínimo completo tiene 4 estados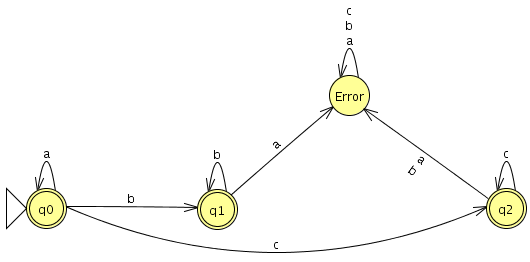

Exámen Setembro de 2005

Dado dos lenguajes regulares L1 y L2 . ¿El lenguaje de intersección L1 ∩ L2 también es un lenguaje regular?
Por las lyes de De Morgan sabemos que

que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular

que es un lenguaje regular, porque la unión de dos lenguajes regulares genera un lenguaje regular

que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular

¿Un autómata finito no–determinista siempre tiene un número menor de estados que un autómata finito determinista asumiendo que ambos aceptan el mismo lenguaje?
No,

¿L+ = L∗ si y solo si ∈ L?

Respuesta

¿Existen lenguajes libres de contexto deterministas que no son regulares?

Verdadero Un lenguaje libre de contexto es generado por una gramática libre de contexto y la gramática $ -> a$b | € genera el lenguaje no regular a^nb^n : N>=0

¿Si un lenguaje es ambiguo todas las gramáticas que generan el lenguaje son ambiguas?

Sí, un lenguaje es ambiguo si todas las gramáticas que generan el lenguaje son ambiguas.

¿Una gramática regular puede ser ambigua?

Si, por ejemplo
$ -> aA | aB
A->b
B->b (es regular y ambigua)

¿Existen expresiones regulares que definen lenguajes que no se pueden aceptar con un autómata finito determinista?
No, porque toda expresión regular se puede transformar en un AFND- y este en un AFD

¿Un autómata finito con pila determinista puede realizar cambios de estados sin cambiar el contenido de la pila?

Si, siempre cuando realice una lectura y para esa lectura solo exista un camino

¿Expresiones regulares definen lenguajes que se pueden aceptar con un autómata finito con pila?

Si, para toda ER existe un AF y por definición todo AF es un AFP en el que la pila no se mueve

¿Para L = L(α) con α = a∗ b∗ , RL tiene índice 4?

Respuesta

Exámen Decembro de 2005

Dado un lenguaje regular L sobre el alfabeto Σ. ¿El lenguaje complementario de L, es decir, Σ∗ − L, también es un lenguaje regular?

L = L1 = Σ*−L1 es regular, porque podemos construir, dado un AFD completo M1 que acepta L1, un AFD M que acepta L simplemente ‘invirtiendo’ sus estados finales, es decir, los estados no finales de M1 serán los estados finales de M y los finales se convierten en los no finales.

¿Existen autómatas finitos no–deterministas que tengan menos estados que sus equivalentes autómatas deterministas mínimos y completos que acepten los mismos lenguajes?
Respuesta

¿La palabra vacia pertenece a cualquier lenguaje formal?

No, porque tiene que pertenecer al subconjunto de las palabras

¿Existen lenguajes libres de contexto deterministas que no sean regulares?

Verdadero Un lenguaje libre de contexto es generado por una gramática libre de contexto y la gramática $ -> a$b | € genera el lenguaje no regular a^nb^n : N>=0

¿Una gramática libre de contexto puede ser ambigua?

Si,

¿Un lenguaje libre de contexto puede ser ambiguo?

Sí, solo podemos afirmar que no son ambiguos los lenguajes regulares. Para que sea ambiguo todas las gramaticas que lo generan deben ser ambiguas

¿Si dos expresiones regulares son diferentes, entonces obviamente definen lenguajes regulares diferentes?
No, dos expresiones regulares pueden definir el mismo lenguaje

¿Si un lenguaje es finito, entonces es regular?

Si porque podemos construir un AF que lo genere con un camino para cada palabra que genere ese lenguaje , entonces el lenguaje es regular.

¿Un autómata finito con pila determinista puede realizar cambios de estados sin cambiar el contenido de la pila?

Si, siempre cuando realice una lectura y para esa lectura solo exista un camino

¿Se puede averiguar si cualquier dos gramáticas de tipo 3 que tienen sistemas de producciones diferentes generan el mismo lenguaje regular?

Sí, obteniendo los AFD-min de ambas gramaticas y comprobando si son iguales generan el mismo lenguaje.

Exámen Xuño de 2006

Dado cualquier gramática G. ¿Se puede hallar siempre una gramática G ambigua que genera el mismo lenguage que G?

Si, porque en toda gramática no ambigua se pueden introducir producciones redundantes para generar una gramática ambigua equivalente

¿Existe una expresión regular que define un lenguaje que se puede aceptar con un autómata finito con pila?

Sí, si tenemos una ER tenemos un AF y por definición un AF es un AFP en el que la pila no se mueve.

Sea ε ∈ L y M un AFND–ε con L(M ) = L. ¿Entonces el estado inicial de M necesariamente es un estado final?

No porque al ser un AFND–ε se puede pasar de un estado a otro sin consumir nada (consumiendo solo ε ) Si fuese AFD o AFND la respuesta seria Si .

¿El AFD mínimo que acepta L tiene tantos estados finales que hay clases de equivalencia de RL que cubren L, (es decir, si unimos las palabras de dichas clases, obtenemos justamente L)?

Respuesta

¿Si Indice(RL ) = ∞, entonces L no es libre de contexto?

Respuesta

Exámen Setembro de 2006

¿Existe un lenguaje regular ambiguo?

Todo lenguaje regular puede ser definido por un AFD-mínimo y un AFD-mínimo se puede transformar en una gramática lineal no ambigua

Sean x, y, y w palabras sobre algún alfabeto. Si x es prefijo de w, e y es sufijo de w y x = y, entonces x = y = w, ¿es verdad?

falso,

Si todos los n > 1 estados de un AFD (autómata finito determinista) completo son estados finales, entonces el AFD no es mínimo.

Si porque al aplicar el algoritmo de minimización todas las casillas quedarian sin marcar por lo que todos los estados serian equivalentes.

Nota : Si en el enunciado no apareciese completo seria Falso.

¿La concatenación de dos lenguajes libres de contexto produce de nuevo un lenguaje libre de contexto?

Respuesta

¿Se puede averiguar si una gramática libre de contexto G genera alguna palabra, es decir, averiguar si L(G) = ∅?

Si comprobando que $ es generativo.

Exámen Decembro de 2006

¿Existe un lenguaje libre de contexto ambiguo?

Respuesta

Sean x, y, y w palabras sobre algún alfabeto. Si x es prefijo de w, e y es sufijo de w y x = y, entonces x = y = w, ¿es verdad?
Respuesta

Si todos los estados de un AFD (autómata finito determinista) completo M son estados finales, entonces el Indice(RL(M ) ) = 1?

Sí, porque en el algoritmo de minimización todas las casillas quedarían sin marcar , siendo todos equivalentes , quedando un solo estado.

¿La intersección de dos lenguajes regulares produce de nuevo un lenguaje regular?

Por las lyes de De Morgan sabemos que

que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular

que es un lenguaje regular, porque la unión de dos lenguajes regulares genera un lenguaje regular

que es un Lenguaje regular, porque el complemento de un lenguaje regular es un lenguaje regular

¿Se puede averiguar si una gramática libre de contexto G genera la palabra vacía, es decir, averiguar si ε ∈ L(G)?

Respuesta

Exámen Xuño de 2007

Si existe una gramática lineal por la izquierda G que genera un lenguaje formal L, entonces L es finito. ¿Es correcto?
No

S -> aB
B -> aB | a

Si una expresión regular no contiene ningún asterisco (de Kleene), entonces el lenguaje es finito. ¿Es correcto?

No, puede contener el operador ⁺

Si un autómata finito determinista mínimo tiene dos estados finales, entonces adicionalmente tiene también por lo menos un estado no final. ¿Es correcto?

Si, porque si son todos estados finales el autómata mínimo estaría compuesto por un único estado final

¿Un autómata finito con pila (no–determinista) que nunca vacía su pila puede aceptar alguna palabra?

Si, por estado final

¿Dada una gramática lineal por la derecha ambigua G, es posible construir una grámatica lineal por la izquierda no–ambigua G que genera el mismo lenguaje, es decir, con L(G ) = L(G)?

Una gramática lineal genera un lenguaje regular y sobre un lenguaje regular se puede generar un autómata y sobre este obtener una gramática lineal por la izquierda no ambigua

Exámen Setembro de 2007

Sean $ −→∗ w y $ −→∗ w dos derivaciones distintas para una palabra w ∈ L ⊂ {a, b, c}∗ y una gramática G con L(G) = L. ¿El lenguage L entonces es ambiguo?

Respuesta

¿Si la unión y el complemento son operaciones cerradas para un tipo de lenguajes formales, entonces la intersección también es una operación cerrada para este tipo?

Respuesta

Para cualquier lenguaje regular L existe un AFND– M con L(M ) = L que contiene un solo estado final. ¿Es correcto?

Si, porque sobre el AFD podemos crear un nuevo estado final incluir transiciones desde el resto de estados finales y transformar los otros estados finales en no finales

Si un autómata finito determinista mínimo tiene dos estados finales, entonces adicionalmente tiene también por lo menos un estado no final. ¿Es correcto?

Respuesta

Una gramática en Forma Normal de Chomsky nunca puede ser ambigua. ¿Es correcto?

Respuesta

Examen Junio de 2008

Sea L un lenguaje regular y , es decir, L₁ contiene un subconjunto de las palabras de L. ¿El lenguaje L₁ entonces es necesariamente regular?

No, es regular y L₁ puede ser libre de contexto

Si dos autómatas finitos deterministas son equivalentes, entonces tienen el mismo numero de estados finales. ¿es correcto?

No.

Si un autómata finito determinista mínimo tiene cuatro estados , por lo menos uno de ellos es un estado no final. ¿Es correcto?

Si, porque si fueran todos finales en la minimización quedaría un único estado final equivalente

Una gramática en Forma Normal de Chomsky puede ser ambigua. ¿Es correcto?

Si, ejemplo:

Examen Diciembre de 2008

¿Existe un lenguaje regular ambiguo?

Un lenguaje ambiguo es aquel que todas las gramáticas que lo generan son ambiguas, pero para todo lenguaje regular se puede crear un AFD mínimo de que obtenemos una gramática no ambigua

Sean x,y, y w palabras sobre algún alfabeto. Si x e y son prefijos de w, entonces x es prefijo y, ¿es verdad?

No,

y=a

x=ab

w=abc

Si todos los estados de un AFD (autómata finito determinista) completo M son estados finales, entonces el Indice(R_L(M)) =1?

Si porque al aplicar el algoritmo de minimización quedaría un único estado final equivalente

¿La unión de dos lenguajes libres de contexto produce de nuevo un lenguaje libre de contexto?

Si partimos de las gramáticas que generan los lenguajes dos lenguajes libres de contexto L1 y L2 podemos crear una nueva gramática donde su símbolo inicial enlace los dos lenguajes $ -> $_L1 | $_L2

¿Se puede averiguar si una gramática libre de contexto G genera alguna palabra, es decir, averiguar si ?

Si, comprobando que el símbolo inicial es generativo.

Examen Junio de 2009

Sea L un lenguaje regular. ¿Existe una gramática lineal por la derecha G que genera L, es decir, L(G)=L, y cuyo numero de variables es igual a Indice(R_L)?

Si una expresión regular contiene un asterisco (de Kleene), entonces el lenguaje es infinito. ¿Es correcto?

No.

Si un autómata finito determinista mínimo (completo) tiene un solo estado no final (a parte de sus estados finales), entonces dicho estado no final (si lo dibujamos) tiene una arista reflexiva. ¿Es correcto?

No. Ejemplo:

¿Para cada autómata finito con pila no determinista (AFPND) que acepta con estado final existe una AFPND que acepta con pila vacía?

Si , porque un AFPND que acepta con pila vacía se puede transformar en AFPND que acepta en estado final y viceversa usando el método de la simulación.

¿Dada una gramática lineal por la derecha ambigua G, es posible construir una gramática lineal por la derecha no ambigua G’ que genera el mismo lenguaje, es decir, con L(G’)=L(G)?

Si. Una gramática lineal por la derecha genera un lenguaje regular y un lenguaje regular se puede modelar con un AFD mínimo , este AFD mínimo puede ser convertido en una gramática lineal por la derecha no ambigua.

Examen Septiembre de 2009

Sea L un lenguaje regular. ¿Existe una gramática lineal por la derecha G que genera L, es decir, L(G)=L, y cuyo numero de variables es igual a Indice(R_L)+5?

Si. Un lenguaje regular es aceptado por un AFD mínimo, con un numero de estados igual al Indice(R_L). Al convertir el AFD mínimo en una gramática lineal por la derecha, cada estado sera una variable. Sobre esta gramática, podemos añadir el numero de variables redundantes que queramos, en este caso 5.

Si una expresión regular contiene un asterisco (de Kleene), entonces el lenguaje es infinito. ¿Es correcto?

No.

No. Ejemplo:

¿Para cada autómata finito con pila no determinista (AFPND) que acepta con pila vacía existe una AFPND que acepta en estado final?

Si , porque un AFPND que acepta con pila vacía se puede transformar en AFPND que acepta en estado final y viceversa usando el método de la simulación.

¿Dada una gramática lineal por la izquierda ambigua G, es posible construir una gramática lineal por la derecha no ambigua G’ que genera el mismo lenguaje, es decir, con L(G’)=L(G)?

Si. Una gramática lineal por la izquierda genera un lenguaje regular y un lenguaje regular se puede modelar con un AFD mínimo , este AFD mínimo puede ser convertido en una gramática lineal por la derecha no ambigua.

Examen Diciembre de 2009

Sea L un lenguaje regular ¿Existe una gramática lineal por la derecha G que genera ?

Si, Si L es regular podemos crear un AFD que acepta el lenguaje, sobre ese AFD aplicando el método del complemento obtenemos un AFD que acepta y a partir de este ultimo AFD podemos crear una gramática linear por la derecha que genera

Si una expresión regular contiene el un asterisco (de Kleene), entonces el lenguaje es infinito. ¿Es correcto?

No.

¿Que se entiende bajo el concepto que una operación entre lenguajes sea una operación cerrada?

Los lenguajes son un tipo de conjuntos. Que una operación sea cerrada quiere decir que cuando esta operación se aplica a elementos de ese conjunto, en este caso a un lenguaje, el resultado sigue estando en ese conjunto, es decir, sigue siendo un lenguaje. Ejemplo: es un lenguaje regular si A,B son lenguajes regulares.

Sea L un lenguaje libre de contexto. ¿Existe un lenguaje L’ tal que sea regular?

Si, es regular y si L es libre de contexto por lo tanto para todo lenguaje L libre de contexto la unión con su complemento genera un lenguaje regular

¿Dada una gramática lineal por la izquierda ambigua G, es posible construir una gramática lineal por la derecha no ambigua G’ que genera el mismo lenguaje, es decir, con L(G’)=L(G)?

26/05/2010

Segundo Examen Practico TALF Modelo 3

Este esta incompleto si algun alma caritativa copio el primer ejercicio lo puede poner en los comentarios.

Ejercicio 2: Describe el lenguaje que genera la siguiente gramática.

Respuesta genera palindromos

Ejercicio 3: Crea una gramática que genere números hexadecimales e indicar el arbol de derivación para 5b3

La gramática que genera números hexadecimales es la siguiente:

abrimos el JFlap y pinchamos en la opción “Grammar”

modelamos la gramática

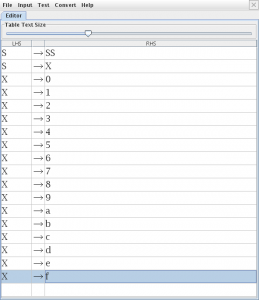para generar el árbol de derivación utilizamos la opción “Brute Force Parse” en el menú “Input” que nos abrirá una nueva pestaña

introducimos 5b3 en la caja de texto y pinchamos en “Start” esperamos que acepte la palabra para luego presionar en el botón “step” hasta obtener el árbol de derivación completo que es el siguiente

26/05/2010

Segundo Examen Practico TALF Modelo 2

1. Comprobar si son equivalentes:

S -> aaS
S -> bB
B -> bB
B -> b

para compara si los anteriores elementos debemos transformar la expresión regular y la gramática en una expresión regular

para la expresión regular los pasos son los siguientes :

Abrimos el JFlap y seleccionamos la Opción “Regular Expression”

insertamos la expresión regular en el JFlap λ

Ahora la convertimos en un autómata con la opción “Convert NFA” del menú “convert”

pinchamos en “Do All” y “Export” lo que nos mostrara una nueva ventana con el autómata equivalente a la expresión regular

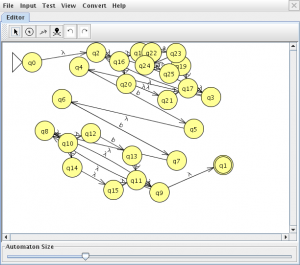guardamos el autómata generado para compararlo después .

Seguidamente modelamos la gramática en JFlap para ello abrimos el JFlap y seleccionamos la opción “Grammar”

modelamos la gramática en la nueva ventana

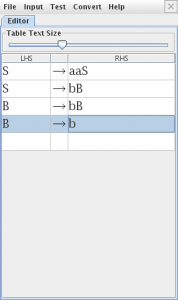como es una gramática lineal por la derecha seleccionamos la opción “Convert Right Lineal Grammar to FA” en el menú “Convert”

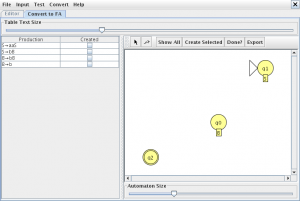pinchamos en “Show All” y “Export” lo que nos creara un autómata equivalente a la gramática

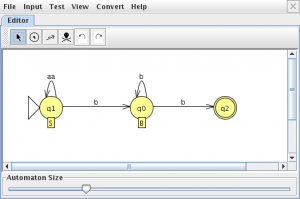ahora con los tres autómatas abiertos vamos a comparar equivalencias

Para comparar la equivalencia entre autómatas seleccionamos la opción “Compare Equivalence” en el menú “Test” lo que nos preguntara con que autómata queremos comparar

El resultado es: La gramática y la expresión regular son equivalentes

2. Dada a seguinte gramática

A -> CB2
A -> 1B
A -> ε
B -> BC
B ->1
C -> 2

a) Transformar a forma normal de Chomsky

modelamos la gramática en JFLAP

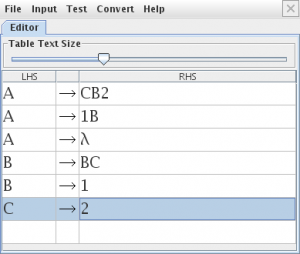Para convertirla a Chomsky seleccionamos la opción “Transform Grammar” en el menú “Convert“, nos advierte que eliminara el símbolo Lambda

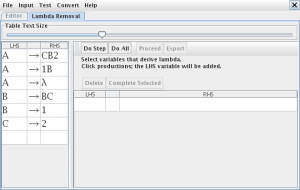pinchamos en “Do All” y “Procceed” y se creara una nueva pestaña

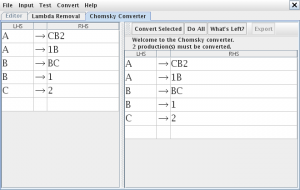Pinchamos en “Do All” y “Export” y aparecerá la gramática convertida a forma normal de Chomsky

b) Convertir a resultante a un autómata de pila polo método LL

Sobre la gramática generada pinchamos en la opción “Convert CFG to PDA (LL)” en el menú “Convert” nos abrirá una nueva pestaña

pinchamos en “Show All” y “Export” lo que nos mostrara el autómata de pila

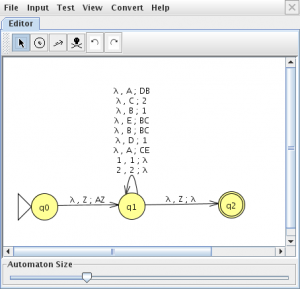c) Obten a traza para a cadea de entrada 1122

Menú “Input” opción “Step by State” abre un dialogo insertamos la cadena 1122 y seleccionamos Final State

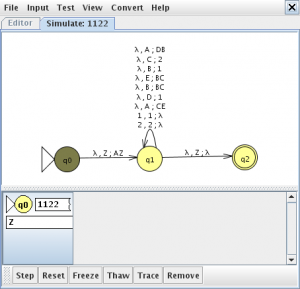le damos a step hasta que aparezca un estado en verde lo seleccionamos y pinchamos en trace la traza final es la siguiente: