1) (1,5 puntos) Dada una muestra aleatoria![]() de una distribución normal de media 16 y varianza 4, calcular el valor b tal que
de una distribución normal de media 16 y varianza 4, calcular el valor b tal que ![]()
2) (1,5 puntos) Encontrar el estimador máximo verosímil para el parámetro ![]() de la función de densidad:
de la función de densidad:
![]() 3)(2 Puntos) El tiempo de acceso (en milisegundos) en situarse una aguja lectora/escritora en un cilindro se supone que sigue una distribución normal. Para determinar en el tiempo medio de acceso se obtuvo una muestra aleatoria de tamaño n=10, con
3)(2 Puntos) El tiempo de acceso (en milisegundos) en situarse una aguja lectora/escritora en un cilindro se supone que sigue una distribución normal. Para determinar en el tiempo medio de acceso se obtuvo una muestra aleatoria de tamaño n=10, con ![]() , cuasivarianza muestral 1,75 .
, cuasivarianza muestral 1,75 .
- Obtener un intervalo de confianza al 75% para
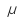 , tiempo medio de acceso. A partir del intervalo anterior obtener el I.C. Para el tiempo medio en segundos.
, tiempo medio de acceso. A partir del intervalo anterior obtener el I.C. Para el tiempo medio en segundos. - ¿Puedo asegurar en cualquier caso que el tiempo medio de acceso está siempre dentro del intervalo. Justifica tu respuesta
- Observando el intervalo, ¿Puedo afirmar que el tiempo medio de acceso es 12ms? Justifica tu respuesta
- Si se mantiene la media y cuasivarianza muestral al aumentar el tamaño muestral ¿Que le ocurre a la longitud del intervalo y a su nivel de confianza? Justifica tu respuesta..
4)(2 puntos) Según el informe del observatorio galego da sociedade da informacion del 2009, el porcentaje de hogares que disponen de conexión de banda ancha a internet es del 38,3% obtenida a partir de una muestra de 1000 hogares En 2008, una muestra de 1200 hogares indico que el 35,3% de los hogares disponían de banda ancha.
- ¿Se justifica la conclusión de que en 2008 hay un porcentaje distinto al 2009 con un nivel de significación del 5%? Responder sin usar el p-valor y calculando en p-valor.
- Si los datos anteriores se mantuviesen constantes el aumentar los tamaños muestrales, como afectaría esta cambio a la decisión del contraste y al valor numérico del p-valor. Justifica tu respuesta.
enjoy
E a solución???
Pois nin idea cando teña tempo buscarei na carpeta dos recordos