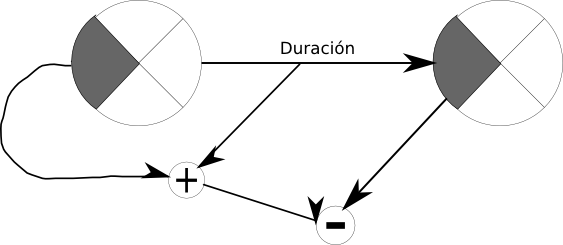
1.- Hacemos una matriz de n+2 filas y n+1 columnas, siendo n el numero de vértices o nudos existentes en el grafo imaginémonos el caso de 8 nodos.
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
|
2.- Rellenamos la matriz con las duraciones de las actividades
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
|
5 |
8 |
4 |
|
|
|
|
|
2 |
|
|
0 |
|
|
10 |
|
|
|
3 |
|
|
|
0 |
6 |
|
|
|
|
4 |
|
|
|
|
7 |
|
|
|
|
5 |
|
|
|
|
|
8 |
12 |
|
|
6 |
|
|
|
|
|
|
|
10 |
|
7 |
|
|
|
|
|
|
|
9 |
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
|
3.- Empezamos rellenando la columnos de Tiempo early siendo el primer tiempo igual a 0
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
|
2 |
|
|
0 |
|
|
10 |
|
|
|
3 |
|
|
|
0 |
6 |
|
|
|
|
4 |
|
|
|
|
7 |
|
|
|
|
5 |
|
|
|
|
|
8 |
12 |
|
|
6 |
|
|
|
|
|
|
|
10 |
|
7 |
|
|
|
|
|
|
|
9 |
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
|
4.- Calculamos el siguiente elemento del tiempo early¿Como? pues muy fácil
Cogemos la columna del elemento que estamos calculando en este caso la 2 y realizamos el siguiente calculo para cada celda con valor (Tiempo Early + Duración de la Actividad)
en este caso es: (0+5)
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
|
3 |
|
|
|
0 |
6 |
|
|
|
|
4 |
|
|
|
|
7 |
|
|
|
|
5 |
|
|
|
|
|
8 |
12 |
|
|
6 |
|
|
|
|
|
|
|
10 |
|
7 |
|
|
|
|
|
|
|
9 |
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
|
En el siguiente paso calculamos la tercera actividad
tenemos los siguientes tiempos
- 1 actividad 0+8=8
- 2 actividad 5+0=5
cogemos la activad cuyo resultado nos de la mayor suma en este caso 8
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
|
4 |
|
|
|
|
7 |
|
|
|
|
5 |
|
|
|
|
|
8 |
12 |
|
|
6 |
|
|
|
|
|
|
|
10 |
|
7 |
|
|
|
|
|
|
|
9 |
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
|
calculo de la cuarta actividad
Nos quedamos con 8 que es el mayor
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
|
5 |
|
|
|
|
|
8 |
12 |
|
|
6 |
|
|
|
|
|
|
|
10 |
|
7 |
|
|
|
|
|
|
|
9 |
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
|
Calculo de la quinta actividad
seleccionamos 15 porque es la mayor
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
|
6 |
|
|
|
|
|
|
|
10 |
|
7 |
|
|
|
|
|
|
|
9 |
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
|
sexta actividad
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
|
7 |
|
|
|
|
|
|
|
9 |
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
|
séptima actividad
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
|
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
octava actividad
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
-> |
|
|
|
|
|
|
|
Ahora copiamos el valor de tiempo early del ultimo nodo en el tiempo last de ese mismo nodo
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
|
|
|
|
|
|
|
|
36 |
séptimo tiempoRestamos al tiempo las de 8 el menor tiempo de la columna
Fila siete tiene el valor 9 para la actividad 8
tiempo last de actividad 8 – valor de nodo
escogemos el mayor
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
|
|
|
|
|
|
|
27 |
36 |
sexto tiempo
Fila 6 tiene valor 10 para actividad 8
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
|
|
|
|
|
|
26 |
27 |
36 |
quinto tiempo
Fila 5 tiene actividad 7 con duracion 12
Fila 5 tiene actividad 6 con duracion 8
Como tenemos dos diferencias cogemos la menor 15
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
|
|
|
|
|
15 |
26 |
27 |
36 |
Cuarto tiempo
Fila 4 tiene los valores 7 para actividad 5
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
|
|
|
|
8 |
15 |
26 |
27 |
36 |
Tercer tiempo
fila 3 tiene valor 0 para actividad 4
fila 3 tiene valor 6 para actividad 5
seleccionamos 8 porque es el menor valor
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
|
|
|
8 |
8 |
15 |
26 |
27 |
36 |
Segundo tiempo
fila 2 tiene valor 0 para actividad 3
8-0=8
fila 2 tiene valor 10 para actividad 6
26-10=16
seleccionamos 8 porque es el menor
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
|
|
8 |
8 |
8 |
15 |
26 |
27 |
36 |
primera fila
fila 1 tiene valor 5 para actividad 2
8-5=3
fila 1 tiene valor 8 para actividad 3
8-8=0
fila 1 tiene valor 4 para actividad 4
8-4=4
escogemos 0 porque es el menor resultado
| Tiempo Early |
J/I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
1 |
|
5 |
8 |
4 |
|
|
|
|
| 5 |
2 |
|
|
0 |
|
|
10 |
|
|
| 8 |
3 |
|
|
|
0 |
6 |
|
|
|
| 8 |
4 |
|
|
|
|
7 |
|
|
|
| 15 |
5 |
|
|
|
|
|
8 |
12 |
|
| 23 |
6 |
|
|
|
|
|
|
|
10 |
| 27 |
7 |
|
|
|
|
|
|
|
9 |
| 36 |
8 |
|
|
|
|
|
|
|
|
| Tiempo Last |
|
0 |
8 |
8 |
8 |
15 |
26 |
27 |
36 |
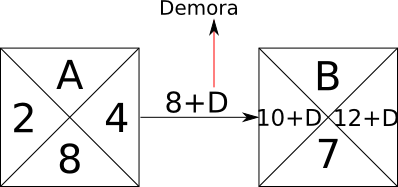 Relación Comienzo\Comienzo si D<8 (8=Duración de la actividad predecesora)
Relación Comienzo\Comienzo si D<8 (8=Duración de la actividad predecesora)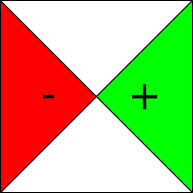 Holgura Libre (Triangulo) El mínimo de (Tiempo mínimo de actividad siguiente – (Tiempo Mínimo de esa actividad+ Valor del Arco))
Holgura Libre (Triangulo) El mínimo de (Tiempo mínimo de actividad siguiente – (Tiempo Mínimo de esa actividad+ Valor del Arco))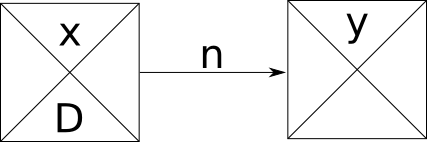 Si n>=D -> Final Comienzo con demora = n-D
Si n>=D -> Final Comienzo con demora = n-D