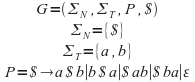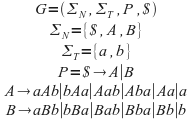P1: Construye una gramática libre de contexto G que genera todas las palabras sobre el alfabeto {a, b} que tienen el mismo número de a’s y b’s, es decir,
L(G) = {ε, ab, ba, aabb, abab, baab, abba, baba, bbaa, aaabbb, aababb, . . .}
La gramática a generada es la siguiente:
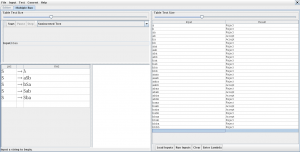
abrimos el JFlap y comprobamos si acepta las palabras del lenguaje
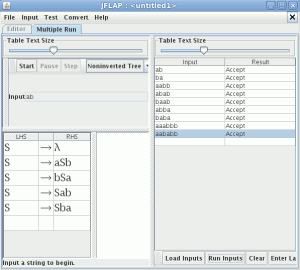generamos un archivo con diversas palabras con los caracteres a y b para verificar que no acepta las palabras que no cumplen la regla
P2: Construye una gramática libre de contexto G que genera todas las palabras sobre el alfabeto {a, b} que tienen un número diferente de a’s y b’s (ayuda: amplía la gramática del primer punto).
Para construir esta gramatica nos basaremos en las producciones anteriores evitando la producción de la palabra vaciá y dividiendo el problema en dos grupos palabras con mayor numero de letras a que de b (A) y palabras con mayor numero de letras b que de a (B). para ello simplemente evitaremos que las producciones terminales de A y B generen ε y permitan introducir un numero ilimitado de as y de bes.
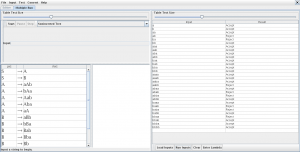
verificamos algunas palabras en el JFlap
