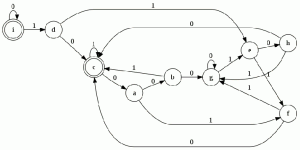
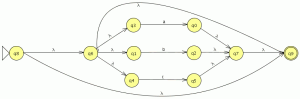
P1: Minimiza el siguiente autómata finito determinista. El estado inicial es el estado a.
Paso 1: eliminamos estados no accesibles.
Un estado no accesible es un estado que no esta relacionado con el conjunto de estados al que pertenece el estado inicial o perteneciendo a este no tiene símbolos de entrada solo de salida. en este caso eliminamos el elemento i, al eliminar el estado i el estado d queda sin símbolos de entrada por lo tanto d tampoco es accesible.
Paso 2: construimos la matriz de estados
matriz de estados
| X/X | ^a | b | *c | e | f | g | h | ||
| ^a | “” | “” | “” | “” | “” | “” | “” | ||
| b | “” | “” | “” | “” | “” | “” | “” | ||
| *c | “” | “” | “” | “” | “” | “” | “” | ||
| e | “” | “” | “” | “” | “” | “” | “” | ||
| f | “” | “” | “” | “” | “” | “” | “” | ||
| g | “” | “” | “” | “” | “” | “” | “” | ||
| h | “” | “” | “” | “” | “” | “” | “” | ||
cada estado es equivalente entre si por lo tanto los descartamos de la misma forma que un triangular de la matriz
| X/X | ^a | b | *c | e | f | g | h | ||
| ^a | ~ | “” | “” | “” | “” | “” | “” | ||
| b | ~ | ~ | “” | “” | “” | “” | “” | ||
| *c | ~ | ~ | ~ | “” | “” | “” | “” | ||
| e | ~ | ~ | ~ | ~ | “” | “” | “” | ||
| f | ~ | ~ | ~ | ~ | ~ | “” | “” | ||
| g | ~ | ~ | ~ | ~ | ~ | ~ | “” | ||
| h | ~ | ~ | ~ | ~ | ~ | ~ | ~ | ||
un estado no final no va a ser equivalente a un estado no final por lo tanto marcamos las celdas donde se relacione un estado final y uno no final
| X/X | ^a | b | *c | e | f | g | h | ||
| ^a | ~ | “” | X | “” | “” | “” | “” | ||
| b | ~ | ~ | X | “” | “” | “” | “” | ||
| *c | ~ | ~ | ~ | X | X | X | X | ||
| e | ~ | ~ | ~ | ~ | “” | “” | “” | ||
| f | ~ | ~ | ~ | ~ | ~ | “” | “” | ||
| g | ~ | ~ | ~ | ~ | ~ | ~ | “” | ||
| h | ~ | ~ | ~ | ~ | ~ | ~ | ~ | ||
llegados a este punto comenzamos a emparejar los estados no marcados:
- (a,b) X
- con 0 vamos a (b,g) no esta marcado no hacemos nada
- con 1 vamos a (f,c) esta marcado por lo tanto marcamos (a,b)
- (a,e) X
- con 0 vamos a (b,h) esta en la diagonal principal no hacemos nada
- con 1 vamos a (f,f) esta en la diagonal principal no hacemos nada
- quedamos a la espera de lo que suceda cuando miremos (b,h)
- (a,f) X
- con 0 vamos a (b,c) como esta marcado marcamos (a,f)
- con 1 vamos a (f,g) como no esta marcado no hacemos nada
- (a,g) X
- con 0 vamos a (b,g) como no esta marcado ni no comprobado esperamos a lo que suceda al comprobar (b,g)
- con 1 vamos a (f,e) que no esta marcado no hacemos nada
- (a,h) X
- con 0 vamos a (b,c) como esta marcado marcamos (a,h)
- 1 no lo miramos porque (a,h) ya se ha marcado
- (b,e) X
- con 0 vamos a (g,h) como no esta marcado no hacemos nada.
- con 1 vamos a (c,f) como esta marcado marcamos (b,e)
- (b,f) X
- con 0 vamos a (g,c) como (c,g) esta marcado marcamos (b,f)
- 1 no lo miramos porque (b,f) ya se ha marcado.
- (b,g) X
- con 0 vamos a (g,g) como esta en la diagonal principal no hacemos nada
- con 1 vamos a (c,e) como esta marcado marcamos (b,g)
- (a,g) estaba a la espera de (b,g) como (b,g) se ha marcado también marcaremos (a,g)
- (b,h) X
- con 0 vamos a (g,c) como (c,g) ya esta marcado marcamos (b,h)
- 1 no lo miramos porque (b,h) ya se ha marcado
- (a,e) estaba a la espera de (b,h) como lo hemos marcado marcamos también (a,e)
- (e,f) X
- con 0 vamos a (h,c) como (c,h) esta marcado marcamos (e,f)
- 1 no lo miramos porque (e,f) ya esta marcado
- (e,g) X
- con 0 vamos a (h,g) o (g,h) como no esta marcado ni comprobado esperamos a comprobar (g,h)
- con 1 vamos a (f,e) o (e,f) como esta marcado marcamos (e,g)
- marcamos también (d,f) y (d,h) porque estaban a la espera de (e,g)
- (e,h) X
- con 0 vamos a (h,c) como (c,h) esta marcado marcamos (e,h)
- 1 no lo miramos porque (e,h) ya se ha marcado
- (f,g) X
- con 0 vamos a (c,g) como ya esta marcado marcamos (f,g)
- 1 no lo miramos porque ya hemos marcado (f,g)
- (f,h)
- con 0 vamos a (c,c) como esta en la diagonal principal lo obviamos
- con 1 vamos a (g,g) como esta en la diagonal principal lo obviamos
- (g,h) X
- con 0 vamos a (g,c) como (c,g) esta marcado marcamos (g,h)
- 1 no lo miramos porque ya hemos marcado (g,h)
Finalmete la matriz queda de la siguiente forma
| X/X | ^a | b | *c | e | f | g | h | ||
| ^a | ~ | X | X | X | X | X | X | ||
| b | ~ | ~ | X | X | X | X | X | ||
| *c | ~ | ~ | ~ | X | X | X | X | ||
| e | ~ | ~ | ~ | ~ | X | X | X | ||
| f | ~ | ~ | ~ | ~ | ~ | X | “” | ||
| g | ~ | ~ | ~ | ~ | ~ | ~ | X | ||
| h | ~ | ~ | ~ | ~ | ~ | ~ | ~ | ||
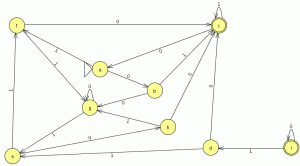
las casillas no marcadas indican estados equivalentes en este caso solo tenemos una casilla no marcada que es (f,h) que nos indica que f es equivalente a h quedando el autómata mínimo de esta forma:
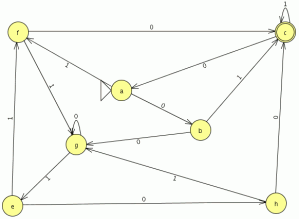
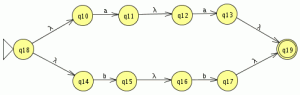
nuestro autómata mínimo esta formado por 7 estados para comprobar si la minimización esta bien realizada minimizamos el automata original en JFlap y comparamos su equivalencia y el numero de estado del autómata mínimo generado, el automata minimo generado es el siguiente:
el numero de estados es el mismo el los dos autómatas y el lenguaje generado es equivalente por lo que debería de estar bien
P2: Determina el Indice(RL) del lenguaje definido por una expresión regular sobre el alfabeto {a, b, c} que define todas las palabras que tengan por lo menos dos a’s consecutivas o por lo menos dos b’s consecutivas (mira hoja 6 si quieres).
Para saber el indice (RL) de la expresión regular tenemos que realizar el siguiente proceso de conversión
Expresión Regular –> AFND-ε –> AFND —> AFD —> AFD mínimo
la expresión regular es (a + b + c)∗ (aa + bb)(a + b + c)∗
el numero de estados del AFD minimo sera el indice del RL en caso que sea completo sino tenemos que sumarle 1 por el estado de error
Paso 1 Expresión Regular a AFND-ε:
Para realizar esta conversión nos basamos en los cinco casos básicos:
- caso 1:para caso “A”
- regla 2:para caso “epsilon”
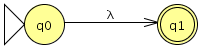
- regla 3:para caso “AB”
- regla 4:para caso “A+B”
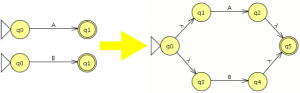
- regla 5:para caso “A*”
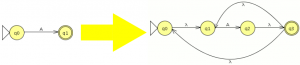
Dividimos la expresión regular en los subconjuntos mínimos a generando un árbol de descomposición.
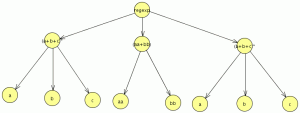empezamos a modelar desde el segundo nivel ya que el primero es muy sencillo
(a+b+c)*
(aa+bb)
unimos los autómatas del segundo nivel y generaremos el automata que describe la expresión regular (a + b + c)∗ (aa + bb)(a + b + c)∗.
comparamos con el JFlap y son equivalentes por lo tanto este paso va bien, ahora eliminamos las transiciones epsilon.
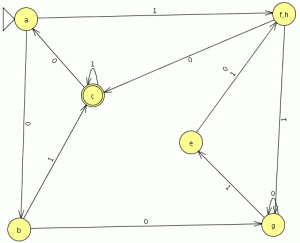
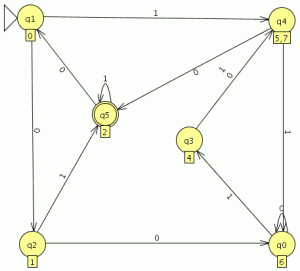
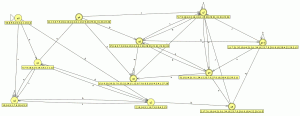Y el AFD generado lo minimizamos
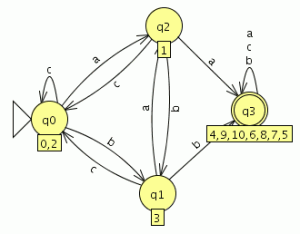como es completo el indice(RL) es igual a 4 , si no fuera completo habría que añadir el estado de error siendo el indice(RL) igual al numero de estados del AFD mínimo + el estado de error