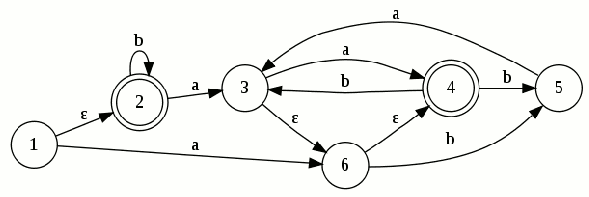
P1: Convierte el siguiente AFND–ε en un AFND (incluye todas las tablas, grafos, quintuplas, y el cálculo de la clausura transitiva necesario). El estado inicial es el estado 1.
Hagamos memoria una quintupla se representa por esta formula ![]() donde:
donde:
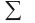 es un alfabeto
es un alfabeto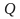 es un conjunto finito no vació de estados
es un conjunto finito no vació de estados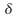 es una función de transición
es una función de transición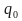 es el estado inicial
es el estado inicial- F es el conjunto de estados finales
Para el AFND–ε la quintupla estará formada por:
Creamos la tabla de transición para el AFND-ε
| Elemento | a | b | |
|---|---|---|---|
|
1 |
{6} | { |
{2} |
|
2 |
{3} | {2} | { |
|
3 |
{4} | { |
{6} |
|
4 |
{ |
{3,5} | { |
|
5 |
{3} | { |
{ |
|
6 |
{ |
{5} | {4} |
ahora calculamos las clausuras para cada elemento
Por clausura de un elemento entendemos el conjunto de estados a los que podemos acceder sin consumir ninguna símbolo , el propio elemento al que le calculamos su clausura pertenecerá a la misma.
para que quede mas claro, para el elemento 3 su clausuara estara compuesta por 3, 6 “(3,ε)=6” y 4 “(6,ε)=4”
| Elemento | a | b | |
clausura |
|---|---|---|---|---|
| 1 | {6} | { |
{2} | {1,2} = Cl(1) |
| 2 | {3} | {2} | { |
{2} = Cl(2) |
| 3 | {4} | { |
{6} | {3,6,4} = Cl(3) |
| 4 | { |
{3,5} | { |
{4} = Cl(4) |
| 5 | {3} | { |
{ |
{5} = Cl(5) |
| 6 | { |
{5} | {4} | {6,4} = Cl(6) |
Ahora creamos una nueva tabla eliminando la columna de ε y substituyendo los estados de destino para cada elemento del alfabeto por la unión de los estados de destino de la clausura. Por ejemplo para el elemento 1 la clausura es {1,2} y para la transición con a debemos incluir 6 para el estado 1 y 3 para el estado 2. por lo tanto nos queda el conjunto {6,3}.
| a | b | |
|---|---|---|
| Cl(1) |
{6,3} |
{2} |
| Cl(2) |
{3} |
{2} |
| Cl(3) |
{4} |
{3,5} |
| Cl(4) | { |
{3,5} |
| Cl(5) |
{3} |
{ |
| Cl(6) | { |
{3,5} |
una vez realizada esta tabla creamos la ultima tabla substituyendo cada estado destino de la tabla anterior por la clausura del mismo
| |
a | b |
|---|---|---|
| Cl(1) |
{3,4,6} |
{2} |
| Cl(2) |
{3,4,6} |
{2} |
| Cl(3) |
{4} |
{3,4,5,6} |
| Cl(4) |
{3,4,5,6} |
|
| Cl(5) |
{3,4,6} |
|
| Cl(6) |
{3,4,5,6} |
Ahora ajustamos los estados para añadir los iniciales y los finales. Si en la clausura de un elemento existe un estado inicial este es inicial (marcados verde en la segunda tabla) y si existe un estado final este es final (marcados de rojo en la segunda tabla) con esto ya tenemos el AFND sin transiciones epsilon
| |
a | b |
|---|---|---|
| *->Cl(1) |
{3,4,6} |
{2} |
| *Cl(2) |
{3,4,6} |
{2} |
| *Cl(3) |
{4} |
{3,4,5,6} |
| *Cl(4) |
{3,4,5,6} |
|
| Cl(5) |
{3,4,6} |
|
| *Cl(6) |
{3,4,5,6} |
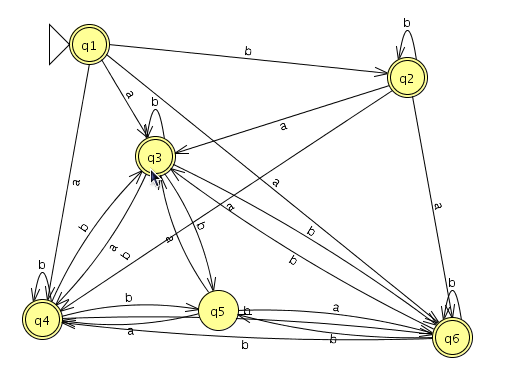
Para el AFND la quintupla estará formada por:
Modelamos el nuevo autómata en JFlap
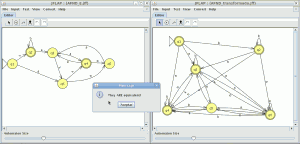
 En la ventana de cualquier autómata seleccionamos el menú test y la opción “compare equivalence” y seleccionamos el otro automata
En la ventana de cualquier autómata seleccionamos el menú test y la opción “compare equivalence” y seleccionamos el otro automata
pinchamos en aceptar y son equivalentes
Gracias tio!!!
Esta página me da la vida
Bueno, aquí está el pesao de turno para darte una nueva solución jajaj. Utilizo un método diferente para obtener dicho autómata equivalente (las tablas son siempre así, solo cambia la forma de transformarla en autómata).
Cogiendo la tabla final, empiezo creando el estado inicial 1, que también será final en este caso. Después, con “a”, iría a un nuevo estado que denomino “3,4,6”, y con “b” a un estado “2”. Podemos decir que el estado “3,4,6” es un conjunto de los estados 3, 4 y 6 del autómata original. Para saber a dónde vamos con “a” desde dicho estado, seguimos el siguiente procedimiento:
– Desde el estado 3 con “a” iríamos al estado 4
– Desde el estado 4 con “a” no iríamos a ningún estado.
– Desde el estado 6 con “a” no iríamos a ningún estado.
Así pues, desde el estado “3,4,6” iríamos, con “a”, al conjunto de los estados a donde iríamos individualmente con 3, 4 y 6, que en este caso sería “4”.
Seguimos el mismo paso para saber a dónde vamos con “b” desde el estado “3,4,6”:
– Desde el estado 3 con “b” vamos al estado “3,4,5,6”.
– Desde el estado 4 con “b” vamos al estado “3,4,5,6”.
– Desde el estado 6 con “b” vamos al estado “3,4,5,6”.
Y por tanto, ya sabemos que desde el estado “3,4,6” iríamos, con “b”, a un nuevo estado que sería “3,4,5,6”.
Se debe realizar dicho procedimiento con cada nuevo “estado de estados” que obtengamos, hasta que hayamos realizado todos los caminos posibles que nos describe la tabla.
Siguiendo dichos pasos se puede obtener un autómata equivalente con tan solo 5 estados (todos finales), los cuales renombramos con letras o números simples para simplificar la nomenclatura (es un poco lioso si tenemos estados con nombres “3,4,5,6” o similares).
Sé que es complicado de entender de forma escrita sin un ejemplo gráfico (además de que no me explico demasiado bien jajaj).
Un saludo!!
todo aporte es bienvenido
Muchas gracias por esta página, no había encontrado una tan buena. Me va a ayudar muchísimo en mi asignatura de Computabilidad y Algoritmia.
Gracias a ti por comentar
Hola tengo una duda en el ejercicio 3 de la práctica 4. Hay que diseñar un AFD usando el método del complemento. Los estados de aceptación del AFD original no serían el q1, q3, q4 y q2?
Si en el AFD complemento lo que se hace es cambiar los estados de aceptación del AFD original por no aceptación y viceversa, por qué en éste AFD tienes como nuevos estados de aceptación el q0 y el q2? En este nuevo AFD el único estado d aceptación no sería el q0? Saludos y gracias.
haces un autómata que solo acepte solo palabras que comiencen por abab.
Después intercambias estados finales por no finales y viceversa