tirando de archivo me encontre unas preguntitas de exámenes prácticos de talf:
Modelar el autómata tal que acepte el lenguaje que contenga palabras con 2 o más pares de ceros consecutivos .
Ej 0000 , 100100100 , 111111001100 , 11111100100100100
Tomado de la corrección en el primer comentario
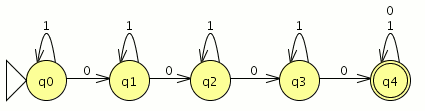
Modelar el autómata tal que acepte el lenguaje que contenga palabras con como mínimo 4 ceros .
Modelar el autómata tal que acepte el lenguaje tal que 
Modelar el autómata tal que acepte el lenguaje tal que 
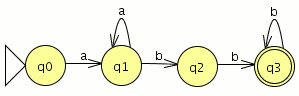
Modelar el autómata tal que acepte el lenguaje tal que acepte todos los binarios excepto los que contengan la subcadena 101.
Lo hacemos por el método del complemento primero modelamos un autómata que acepte palabras que contengan la subcadena 101.
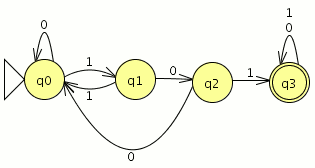aplicamos el metodo del complemento (los estados finales se transforman en no finales y viceversa)
Modelar el autómata tal que acepte el lenguaje binario tal que la tercera cifra por la derecha sea distinta a la segunda cifra por la izquierda.
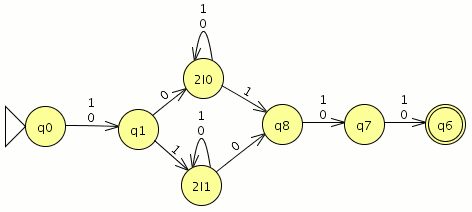Dado un alfabeto {a, b, c}, construir un AFD que acepte aquellas palabras que contengan al menos dos ‘a’, una ‘b’ y una ‘c’
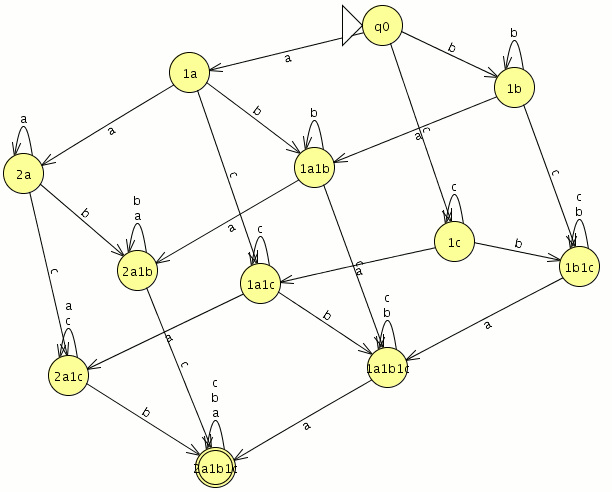teneis aqui el Autómata
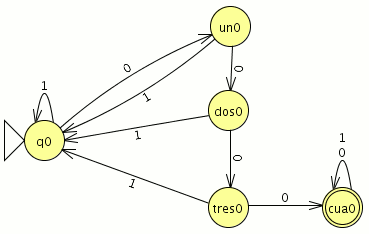
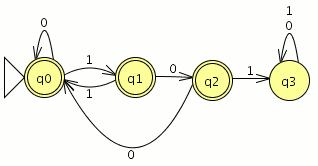
como verás la imágen del primer autómata es erronea, la solución correcta sería la siguiente que es un AFD completo que acepta palabras con 2 o más pares de ceros consecutivos. En otras palabras, cualquier palabra con un número par de ceros consecutivos > 4 ceros son aceptadas. Ejemplos:
0000–> palabra mínima aceptada.
1000001-> acepta tiene un número de 2 pares de ceros consecutivos.
En resumen tenemos que aceptar cualquier palabra que contenga almenos la cadena “0000” porque ya tendría 2 pares de ceros consecutivos.
jgalonso creo que te falta una transicion en el estado q4 sobre si mismo con el simbolo 0 sino se muere ahí. Saludos!
premio, pues falta esa transición cuanto tenga tiempo lo arreglo
arreglado
la ultima cadena de ese aceptor es 00001* ,
q2 ya indica que ingreso un par de ceros. un bucle alli de uno estaría bien. en q4 , ya hay dos pares de ceros, un bucle con cero..
Suerte Saludos.