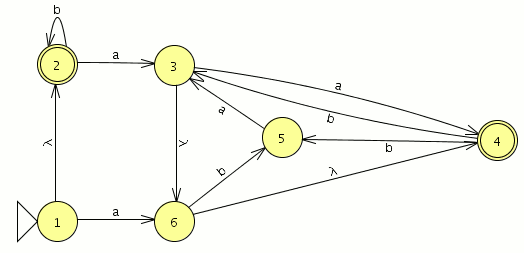
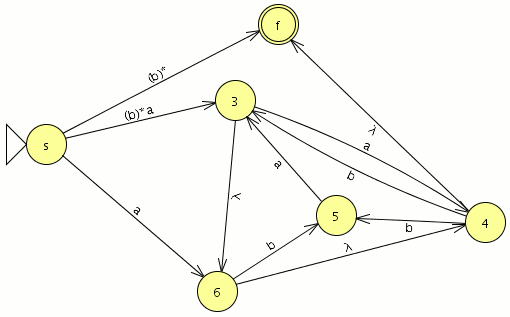
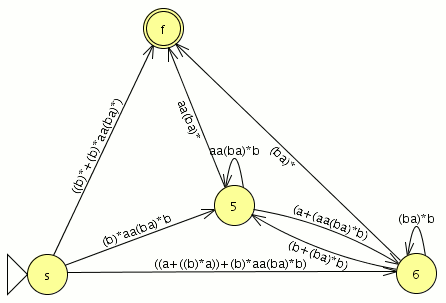
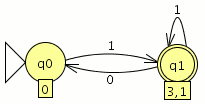
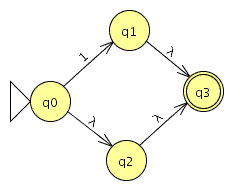
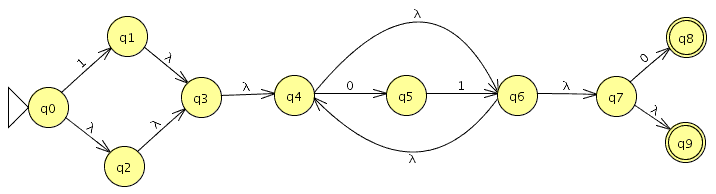
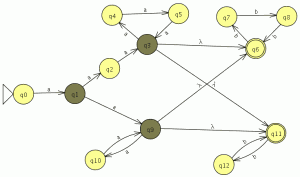
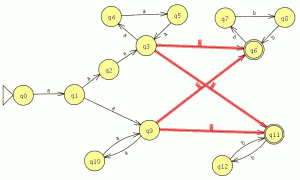
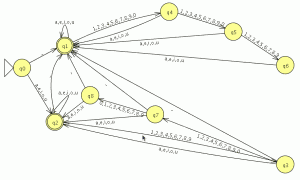
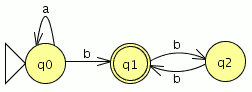P1: Sea C = {a,b,c,d,e,f,g,h} un conjunto (de letras), y sea R = {(a, d), (b, e), (c, a), (d, b), (e, c), (f, g), (g, h)} ⊂ C × C una relación sobre C.
- Construye las relaciones Ri para todos los i = 0, . . . , ∞.
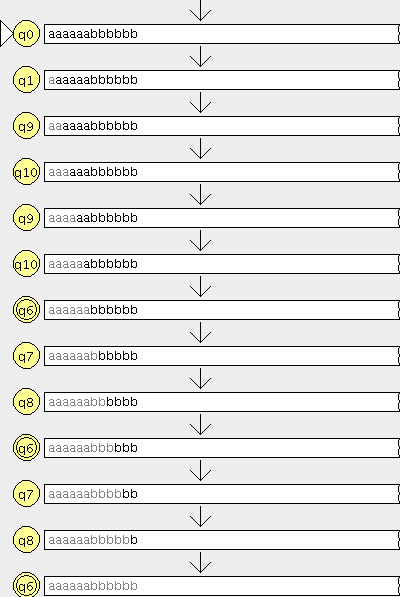
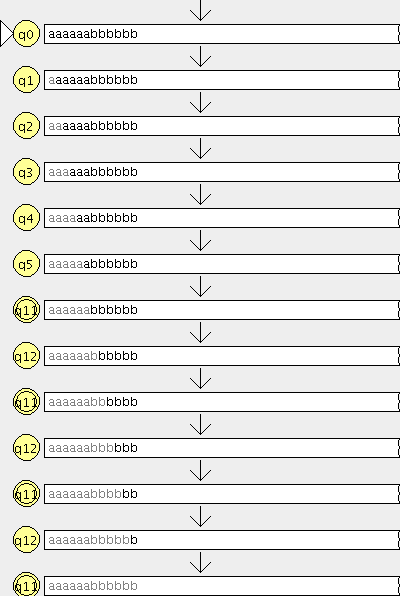
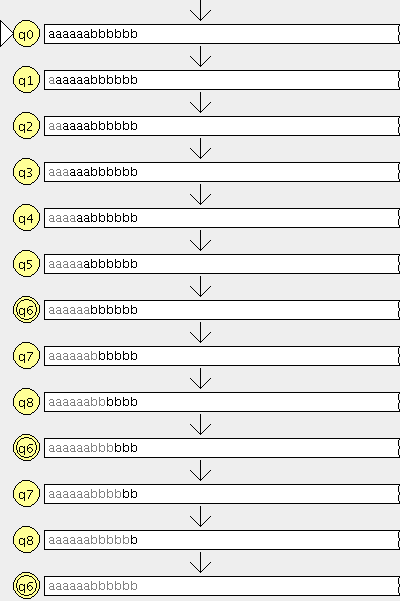
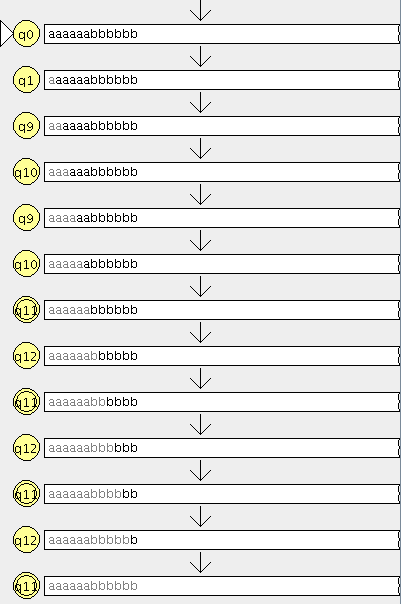
- R0 ={(a,a),(b,b),(c,c),(d,d),(e,e),(f,f),(g,g),(h,h)} (Las relaciones de todos los elementos consigo mismo)
- R1={(a,d),(b,e),(c,a),(d,b),(e,c),(f,g),(g,h)} (La relación que nos dan)
- (a,d) de R1 y (d,b) de R1 generan (a,b).
- (b,e) de R1 y (e,c) de R1 generan (b,c).
- (c,a) de R1 y (a,d) de R1 generan (c,d).
- (d,b) de R1 y (b,e) de R1 generan (d,e).
- (e,c) de R1 y (c,a) de R1 generan (e,a).
- (f,g) de R1 y (g,h) de R1 generan (f,h).
- (g,h) de R1 no genera nada.
- R2={(a,b),(b,c),(c,d),(d,e),(e,a),(f,h)} <–( la unión de las relaciones generadas en R1)
- (a,b) de R2 y (b,e) de R1 generan (a,e).
- (b,c) de R2 y (c,a) de R1 generan (b,a).
- (c,d) de R2 y (d,b) de R1 generan (c,b).
- (d,e) de R2 y (e,c) de R1 generan (d,c).
- (e,a) de R2 y (a,d) de R1 generan (e,d).
- (f,h) de R2 no genera nada
- R3={(a,e),(b,a),(c,b),(d,c),(e,d)} <– ( la unión de las relaciones generadas en R2)
- (a,e) de R3 y (e,c) de R1 generan (a,c).
- (b,a) de R3 y (a,d) de R1 generan (b,d).
- (c,b) de R3 y (b,e) de R1 generan (c,e).
- (d,c) de R3 y (c,a) de R1 generan (d,a).
- (e,d) de R3 y (d,b) de R1 generan (e,b).
- R4={(a,c),(b,d),(c,e),(d,a),(e,b)} <– (la unión de las relaciones generadas en R3)
- (a,c) de R4 y (c,a) de R1 generan (a,a).
- (b,d) de R4 y (d,b) de R1 generan (b,b).
- (c,e) de R4 y (e,c) de R1 generan (c,c).
- (d,a) de R4 y (a,d) de R1 generan (d,d).
- (e,b) de R4 y (b,e) de R1 generan (e,e).
- R5={(a,a),(b,b),(c,c),(d,d),(e,e)} <– (la unión de las relaciones generadas en R4)
- (a,a) de R5 y (a,d) de R1 generan (a,d).
- (b,b) de R5 y (b,e) de R1 generan (b,e).
- (c,c) de R5 y (c,a) de R1 generan (c,a).
- (d,d) de R5 y (d,b) de R1 generan (d,b).
- (e,e) de R5 y (e,c) de R1 generan (e,c).
- R6={(a,d),(b,e),(c,a),(d,b),(e,c)} <– (la unión de las relaciones generadas en R5)
- (a,d) de R6 y (d,b) de R1 generan (a,b).
- (b,e) de R6 y (e,c) de R1 generan (b,c).
- (c,a) de R6 y (a,d) de R1 generan (c,d).
- (d,b) de R6 y (b,e) de R1 generan (d,e).
- (e,c) de R6 y (c,a) de R1 generan (e,a).
- R7={(a,b),(b,c),(c,d),(d,e),(e,a)} <– (la unión de las relaciones generadas en R6)
- (a,b) de R7 y (b,e) de R1 generan (a,e).
- (b,c) de R7 y (c,a) de R1 generan (b,a).
- (c,d) de R7 y (d,b) de R1 generan (c,b).
- (d,e) de R7 y (e,c) de R1 generan (d,c).
- (e,a) de R7 y (a,d) de R1 generan (e,d).
- R8={(a,e),(b,a),(c,b),(d,c),(e,d)} ==R3 <– (la unión de las relaciones generadas en R7)
- R9==R4
- R10=R5
- R11=R6
- R12=R7
- R13=R3
- Rn= R (n-3) mod 5+3
- Construye la relación R∗.
Basta con unir todas las relaciones hasta R5 ( a partir de R7 el resto estarán repetidas y R5,R6 y R7 son subconjuntos)
R*={(a,a),(b,b),(c,c),(d,d),(e,e),(f,f),(g,g),(h,h),(a,d),(b,e),(c,a),(d,b),(e,c),(f,g),(g,h),(a,b),(b,c),(c,d),(d,e),(e,a),(f,h),(a,e),(b,a),(c,b),(d,c),(e,d),(a,c),(b,d),(c,e),(d,a),(e,b)}
- Argumenta si R∗ es reflexiva, simétrica , y/o transitiva.
- Reflexiva: Si porque todo elemento estan relacionados consigo mismo al pertenecer R0 a R*.
- Simétrica:
- (a,d) y (d,a) V
- (b,e) y (e,b) V
- (c,a) y (a,c) V
- (d,b) y (b,d) V
- (e,c) y (c,e) V
- (f,g) no existe (g,f) F
- (g,h) no existe (h,g) F
- (a,b) y (b,a) V
- (b,c) y (c,b) V
- (c,d) y (d,c) V
- (d,e) y (e,d) V
- (e,a) y (a,e) V
- (f,h) no existe (h,f) F
- Transitiva: Si, porque hemos relacionado todas los pares entre si
- ¿Cuál pareja (o parejas) deberíamos añadir a la relación R para que R∗ sea simétrica (si piensas que R∗ no es simétrica en el apartado anterior)?
- (g,f), (h,g) y (h,f)