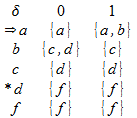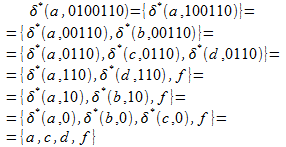TALF Hoja 4 (16 de Marzo de 2010)
P1: Convierte el AFND de la hoja anterior en un autómata finito determinista. Incluye en tu solución la tabla de conversión tal como lo vimos en clase, la quintupla del AFD obtenido finalmente, y su grafo.
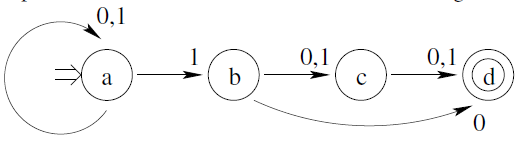
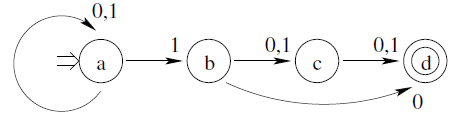
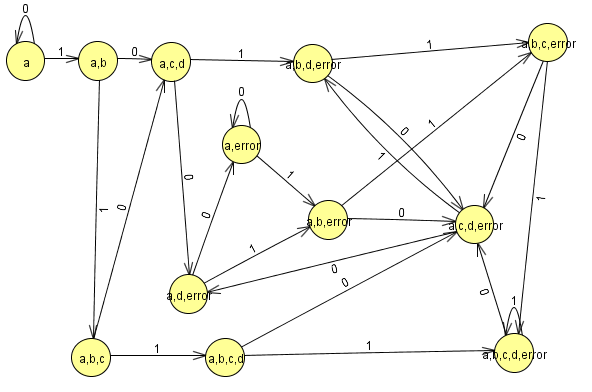
Partimos del siguiente AFND.
Añadimos el estado de Error.
Comenzamos a crear la tabla de conversión
partimos del estado inicial {a}. con 0 vamos a {a} y con 1 a {a,b}
{a} ya pertenece al conjunto de estados, pero {a,b} no por lo tanto añadimos el estado {a,b}.
en el conjunto {a,b} con valor 0 a nos lleva a {a} y b nos lleva a {c,d} por lo tanto {a,b} con 0 nos lleva a {a,c,d} como {a,c,d} no esta en el conjunto de estados lo añadimos y añadimos las transiciones.
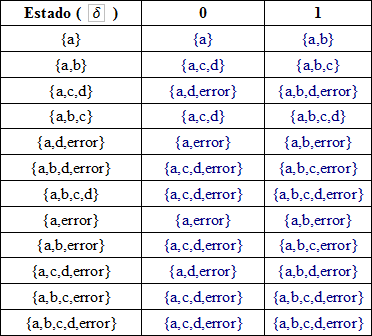
repetimos el procedimiento hasta que no se creen mas elementos para el conjunto de estados. quedándonos la siguiente tabla (a menos que me haya equivocado)
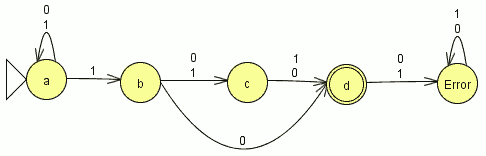
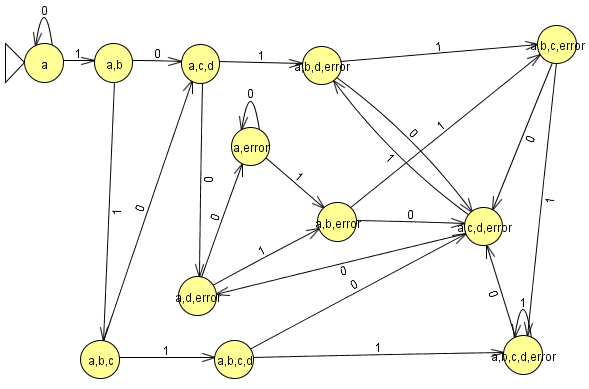
ahora pasamos la tabla a un grafo.
Los primeros estados iniciales de nuestro AFND “con los que empezamos la tabla” son nuestros estados iniciales, en esta caso A.
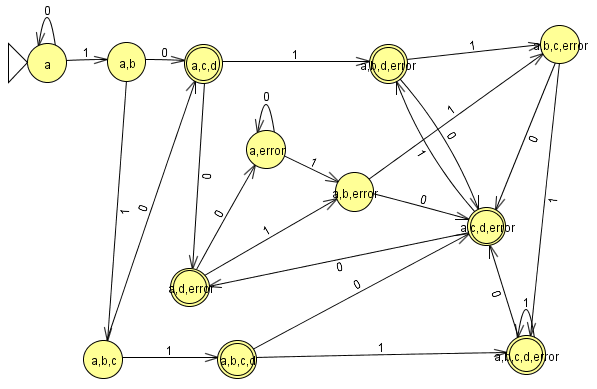
Todo estado del AFD donde exista un estado final del AFND es final (en este caso todos donde este d)
Finalmente la quintupla queda definida por:
M=(∑,Q,δ,q0,F)
siendo
- ∑ El alfabeto
- Q Conjunto finito de estados
- δ la función de transición
- q0 conjunto de estados iniciales
- F conjunto de estados finales
por lo tanto para este AFD la quintupla sera:
- ∑ {0,1}
- Q [{a},{a,b},{a,c,d},{a,b,c},{a,d,error},{a,b,d,error},{a,b,c,d},{a,error},{a,b,error},{a,c,d,error},{a,b,c,error},{a,b,c,d,error}]
- δ es la tabla de transiciones
- q0 {a}
- F [{a,c,d},{a,d,error},{a,b,d,error},{a,b,c,d},{a,c,d,error},{a,b,c,d,error}]
Hoja 3 (9 de Marzo de 2010)
P1: Calcula, paso a paso, el resultado de la función 
para el autómata de la hoja anterior y la palabra de entrada w=0100110, es decir, 
.
w=0100110
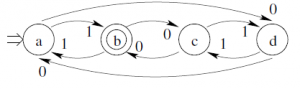
P2: Escribe la tabla para la función de transición 
del AFND con el siguiente grafo:
Calcula, paso a paso, el resultado de la función para este autómata y la palabra de entrada w=0100110, es decir, . Averigua una palabra sobre {0,1} que el autómata no acepta.
Como 
el autómata acepta.
Una palabra que el autómata no aceptaria seria cualquiera que acabara con mas de dos ceros.
Gracias a melasuda por la resolución.
Practica 2 TALF
Modelar la gramática en JFlap
| Acción |
Abreviatura |
| S | A |
| PAÑAL_SUCIO | B |
| FRÍO | C |
| CAMBIO_POSTURA | D |
| GASES | E |
| HAMBRE | F |
| DOLOR | G |
| BIENESTAR | H |
| CONT_PS | I |
| PATALEO_PS | J |
| CONT_FRÍO | K |
| CONT_CP | L |
| BOCA_HAMBRE | M |
| quejido | a |
| para_quejido | b |
| llanto_medio | c |
| pataleo | d |
| estiramiento_pierna | e |
| ceño_fruncido | f |
| encoger_cuerpo | g |
| llanto_alto | h |
| llanto_bajo | i |
| giro_lento_cabeza | j |
| ojos_abiertos | k |
| boca_abierta | l |
| chupeteo_pausado | m |
| puños_apretados | n |
| giro_rápido_cabeza | o |
| cuerpo_relajado | p |
| sonrisa | q |
Producciones
A→B|C|D|E|F|G|H
B→abI
I→abI|cJ
J→d|e|dJ|eJ
C→abK
K→abK|cfg
D→abL
L→abL|cd
E→hgf
F→ijkM
M→lM|mM|ε
G→hdnflo
H→pqm
Comprobar si las siguientes sentencias pertenecen al lenguaje generado y en caso afirmativo hallar su árbol de derivación, y averiguar qué le está pasando al bebé.
Quejido para_quejido quejido para_quejido llanto_medio pataleo pataleo
estiramiento_pierna pataleo
Se corresponde con: ababcdded <– Acepta
Podría significar que el bebé tiene calor.
Llanto_bajo giro_lento_cabeza ojos_abiertos boca_abierta boca_abierta chupeteo_pausado chupeteo_ pausado boca_abierta
Se corresponde con: ijkllmml <- Acepta
Podría significar que el bebé tiene sed.
Inventar una sentencia válida y otra inválida.
VALIDA
abcde
INVALIDA
acll
Construir una posible regla de producción para comunicar MIEDO
Miedo = N
N ->llanto_alto encoger_cuerpo ceño_fruncido quejido
N ->hgfa
Ejercicio 2 Teoria TALF
p1: Dados dos lenguajes 
y 
sobre el alfabeto 
. Anotamos con 
la unión, con 
la intersección, 
el complemento y con 
la diferencia.
Verifica o contradice:
- Cierto: supongamos que es un lenguaje que genera palabras de la forma
comprenderá todas las palabras sobre el alfabeto excepto las que cumplan la forma si a 
le sacamos el sublenguaje generado por obtendremos el mismo resultado.
- Cierto: supongamos que
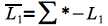
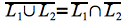
- cierto:supongamos que 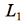es un lenguaje que genera palabras de la forma 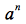y que 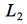genera el lenguaje
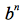por lo tanto 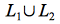generaran un lenguaje de la forma 
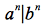por lo tanto 
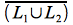serán todas las combinaciones del lenguaje 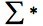excepto las que cumplan con el patrón .
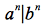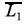serán todas las palabras del lenguaje 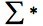excepto las que cumplan la forma .
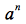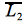serán todas las palabras del lenguaje 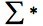excepto las que cumplan la forma .
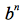por lo tanto la intersección de ambos lenguaje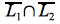
serán todas las palabras de 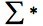excepto las que cumplan el patrón .
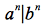- cierto:supongamos que
- cierto: La intersección de y serán las palabras comunes entre los dos sublenguajes y su complemento sera
para la segunda parte de la ecuación 
- cierto: La intersección de
- Falso con
generaríamos palabras de la forma 
y con 
generaríamos palabras de la forma 
.
- Falso con
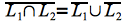
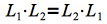
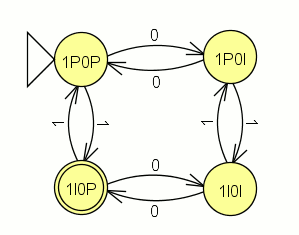
p2: Construye un autómata finito determinista que “acepta” el lenguaje L que contiene todas las palabras (finitas) sobre el alfabeto {0, 1} con un número par de 0s y un número impar de 1s.
El modelo del autómata en JFlap lo podéis descargar en este enlace: autómata practica 2
Edit: Corregido el autómata que tenia mal un enlace, un 0 en lugar de un 1. Muchas gracias a Ymourino
Practica 1 Talf
Búsquedas basadas en Expresiones Regulares
El objetivo de la práctica es utilizar herramientas del sistema operativo como por
ejemplo Word en Windows para hacer búsquedas en archivos .doc; y greo o egrep
para buscar en archivos de texto plano.
Buscar en el “Himno Galego” o “Conxuro da Queimada” usando Word.
- Palabras completas. Por ejemplo “de” “dos” “terra” o cualquiera que se te ocurra.
- <na>
<dos>
<terra>
- <na>
- Palabras que comiencen por una letra o conjunto de ellas. Por ejemplo palabras que comiencen por “de”.
- <de
- Que además de comenzar por un conjunto de letras, estén al principio de una línea. Líneas que empiecen por “de”.
- ^v<de
- Palabras que terminen con una letra o conjunto de letras. Por ejemplo, palabras que terminen en “os” o “en”.
- os>^l
en>^l
- os>^l
- Que además de terminar en un conjunto de letras estén al final o al principio de una línea.
- >as^| (no funciona)
- Palabras que tienen dos vocales “a”.
- [a-z,A-Z]@a[a-z,A-Z]@a
Buscar en el archivo de personas que contienes nombres de personas e información adicional sobre ellas (correo, ciudad, teléfono). Usando grep.
- Personas que se llaman Carlos, mostrando la línea que ocupan en la lista.
- cat personas.txt | grep -n “Carlos”
- Personas cuyo nombre comience por las letras comprendidas entre M y S.
- cat personas.txt | grep -n “[MS]”
- Líneas del archivo de personas que contengan por lo menos diez letras mayúsculas consecutivas.
- cat personas.txt | grep “[A-Z][A-Z][A-Z][A-Z][A-Z][A-Z][A-Z][A-Z][A-Z][A-Z]”
- Líneas que tengan su dirección de correo electrónico en el servidor uvigo.
- cat personas.txt | grep “@uvigo”
- Personas cuyo nombre comience por la letra “E” o “M”.
- cat personas.txt | grep “^[EM]”
- Personas cuyo número de teléfono termine en 21.
- cat personas.txt | grep “21$”
- Personas cuyo prefijo de teléfono sea el 988
- cat personas.txt | grep ” 988″
- Otras búsquedas que se te ocurran.
Expresiones Regulares con MySQL
Elementos
Operativa
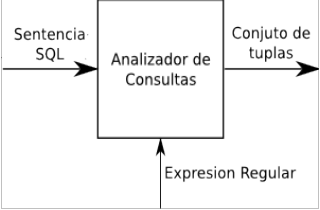
Para interactuar con el sistema se envían las consultas sql al analizador de consultas este separa la consulta en parte y analiza la expresión regular
Sintaxis:
| Tipo de Operador | Ejemplos | Descripción |
|
Caracteres Literales. Coincidencia exacta |
a A y 6 % @ | Caracteres, Digitos y algunos caracteres especiales que coincidan exactamente |
| \$ \^ \+ \\ \? | Precedencia de un carácter especial con \ para cancelar su significado como expresion regular | |
| \n \t \r | Nueva linea, tabulador o enter | |
| \cJ \cG | Codigos de Control | |
| \xa3 | Codigos hexadecimales para cualquier carácter. | |
|
Anclajes |
^ | El campo empieza por |
| $ | El campo acaba por | |
| [[:<:]] | La palabra empieza por | |
| [[:>:]] | La palabra acaba por | |
|
Grupos de caracteres, cualquier carácter del grupo |
[aAeEiou] | Cualquier carácter contenido en [] |
| [^aAeEiou] | Cualquier carácter excepto los contenidos en [] | |
| [a-fA-F0-9] | Cualquier carácter hexadecimal (0 a 9 o a hasta f) | |
| . | Cualquier caracter | |
| [[:space:]] | Cualquier carácter separador (espacio \n \r o \t) | |
| [[:alnum:]] | Cualquier carácter alfanumerico | |
|
Contadores, actuan sobre elementos previos |
+ | 1 o mas |
| * | 0 o mas | |
| ? | 0 o 1 | |
| {4} | Exactamente 4 | |
| {4,} | 4 o mas | |
| {4,8} | Entre 4 y 8 | |
| Añadir una ? Después de cualquier contador para convertirlo | ||
| Alternación | | | o |
| Agrupamiento | () | Grupo para contar y guardar la variable |
Ejemplos:
Actores cuyo nombre acabe por la letra A
SELECT * FROM actor where first_name REGEXP ‘A$’
Actores que hayan participado en peliculas de animación
SELECT * FROM actor_info where film_info REGEXP ‘Animation:’
Actores que hayan participado en peliculas de animación pero no en peliculas de Accion
SELECT * FROM actor_info where film_info REGEXP ‘Animation: ‘ and not film_info REGEXP ‘Action:’
Todas las peliculas que tengan escenas eliminadas
SELECT * FROM film where special_features regexp ‘Deleted Scenes’ and not special_features regexp ‘trailers’
Todas las direcciones que sean Lane
SELECT * FROM address where address regexp ‘lane’
Todos los alquileres del mes 5 del 2005
SELECT * FROM rental r where rental_date regexp ‘^2005-05’ order by rental_date ASC
Actores cuyo nombre tenga dos vocales seguidas
SELECT * FROM actor a where first_name regexp ‘((a|e|i|o|u){2})’
Fuentes
http://www.wellho.net/regex/mysql.html