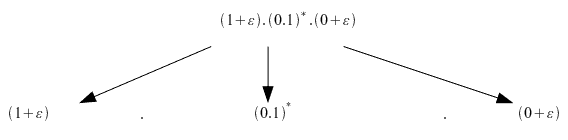P1: ¿Qué lenguajes definen las siguientes expresiones regulares?
- Expresión regular numero 1: (((0.1)∗ + (0.1)∗ .0) + ((1.0)∗ + (1.0)∗ .1))
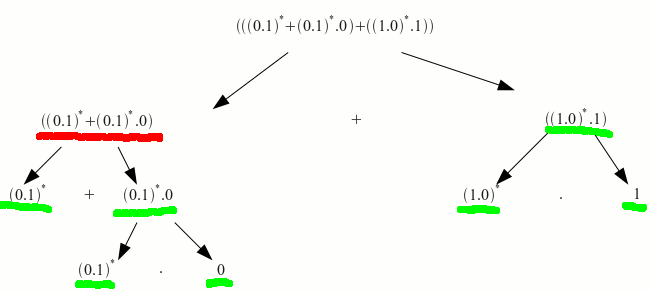
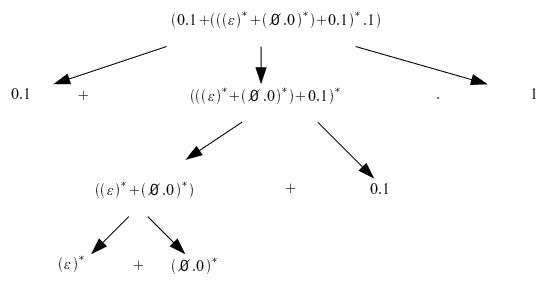
Descomponemos la expresión regular
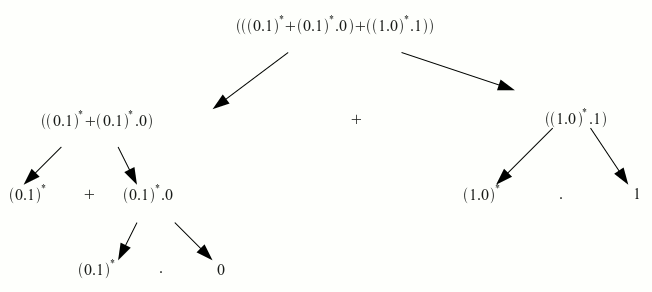 empezamos a descomponer la expresión regular a partir de los nodos finales (marcados en rojo).
empezamos a descomponer la expresión regular a partir de los nodos finales (marcados en rojo).
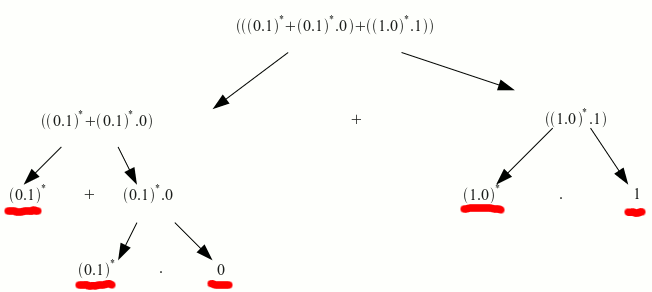 Paso 1: intentamos minimizar los nodos finales: en esta expresión no se puede
Paso 1: intentamos minimizar los nodos finales: en esta expresión no se puede
Paso 2:Describimos el lenguaje de cada nodo final:
subimos al nivel anterior y unimos los nodos en los que sus elementos siguientes estén descritos hasta que lleguemos a la raíz del árbol.
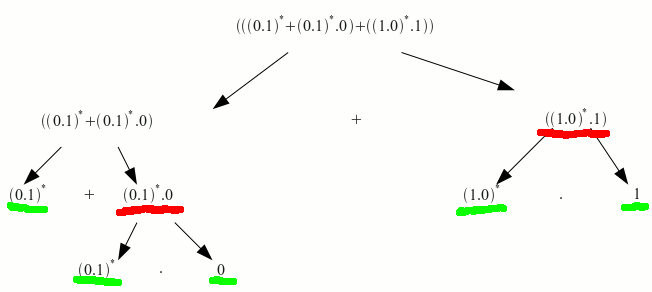 miramos si podemos minimizar los nodos a describir (marcados de rojo), en este caso no podemos.
miramos si podemos minimizar los nodos a describir (marcados de rojo), en este caso no podemos.
asi que describimos los nodos en los que nos encontramos
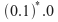 : cero o mas repeticiones de la cadena 01 unidas con 0
: cero o mas repeticiones de la cadena 01 unidas con 0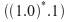 :cero o mas repeticiones de la cadena 10 unidos con 1
:cero o mas repeticiones de la cadena 10 unidos con 1
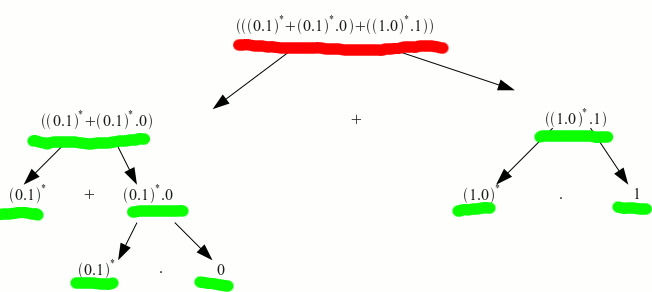
nueva iteración. subimos al nivel superior
miramos si podemos minimizar los nodos a describir (marcados de rojo), en este caso no podemos.
asi que describimos los nodos en los que nos encontramos
subimos
Describimos la expresión regular uniendo los elementos anteriores (+=0) (*=y)
cero o mas repeticiones de la cadena 01 ó cero o mas repeticiones de la cadena 01 unidas con 0, o cero o mas repeticiones de la cadena 10 unidos con 1
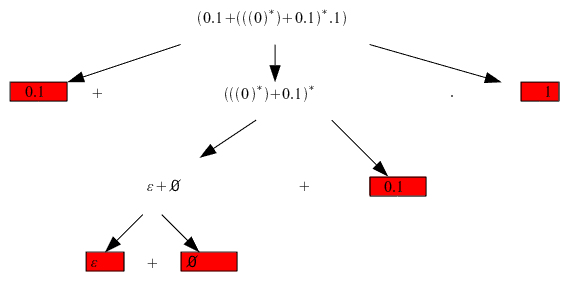
Paso 1: Descomponemos la expresión regular en pequeñas expresiones.
marcamos los nodos finales
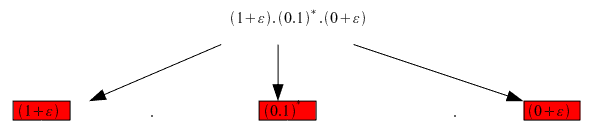 Minimizamos los nodos finales, en este caso no se puede
Minimizamos los nodos finales, en este caso no se puede
Describimos los nodos finales
subimos al siguiente nivel de la estructura
intentamos minimizar la expresión actual: no se puede
Describimos la expresión actual.
Paso 1: Descomponemos la expresión regular en pequeñas expresiones.
marcamos los nodos finales
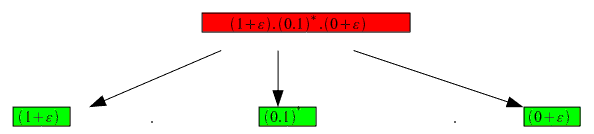
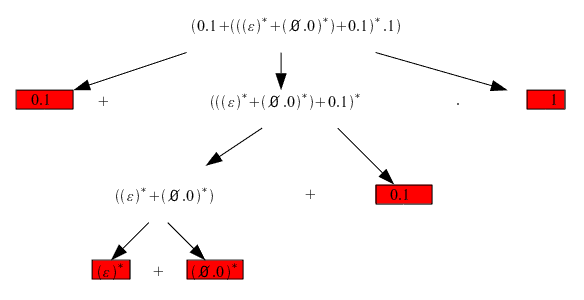 intentamo minimizar algún nodo final en este caso si que podemos
intentamo minimizar algún nodo final en este caso si que podemos
empezamos a minimizar hacia arriba y nos queda la siguiente expresión minimizada
describimos las expresiones del segundo nivel
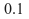 : la cadena 01
: la cadena 01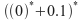 : cero o mas repeticiones de la cadena con 0 o mas repeticiones de cero o de la cadena 01
: cero o mas repeticiones de la cadena con 0 o mas repeticiones de cero o de la cadena 01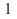 : la cadena 1
: la cadena 1
por lo tanto el lenguaje que define esta expresión regular es: la cadena 01 o cero o mas repeticiones de la cadena con 0 o mas repeticiones de cero o de la cadena 01 unido a la cadena 1
P2: Escribe una expresión regular sobre el alfabeto {a, b, c} que define todas las palabras que tengan dos a’s consecutivos o dos b’s consecutivos.
(a+b+c)*.((aa)+(bb)).(a+b+c)*
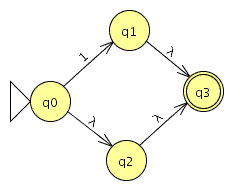
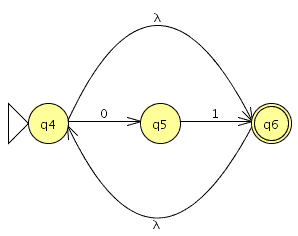
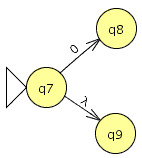
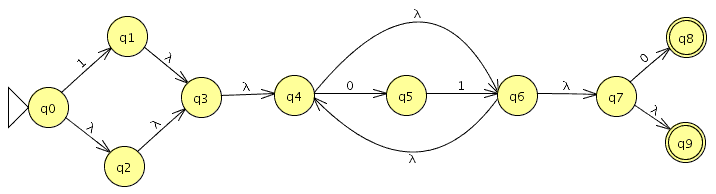
P3: Construye según procedimiento visto en clase un AFND–ε que acepta las mismas palabras que define la expresión regular de P1 apartado 2.
modelamos las pequeñas expresiones el las que hemos descompuesto la expresión 2:
Ahora unimos las partes en un autómata .