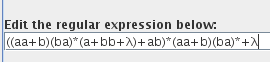EJERCICIOS
Inicialmente debes construir un nuevo proyecto (practica4). Una vez creado, copia en el directorio de trabajo los ficheros examinar.c, examinar.h y la librería creada en la práctica anterior glig.c con su fichero prototipo glig.h. Añádelos al proyecto (por supuesto, acuérdate de añadir también las librerías glu32.lib, glut.lib y opengl32.lib).
1. Para la realización de esta práctica vas a necesitar una nueva primitiva que dibuje un cono. Añádela a tu librería glig.c.
void igWireCone (int pu, int pv); /* s1= 2.0, s2= 1.0, uMax= 1.0, vMax= 0.5 */
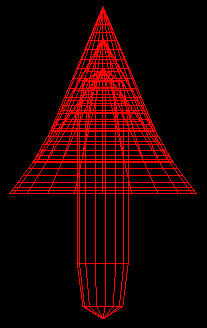
2. Utiliza las primitivas de la librería glig.c, para construir un abeto como el de la figura, sin utilizar las funciones glPushMatrix() y glPopMatrix(). Para ello crea una display list como en el ejemplo e introduce en su definición el código necesario para dibujar el abeto:
void CreaAbeto (void)
{
abeto = glGenLists (1);
if (abeto != 0) /* Cero no es un identificador valido para una display list */
{
glNewList (abeto, GL_COMPILE);
/* Código para dibujar el abeto */
glEndList ();
}
}
Los pasos a seguir para dibujar el abeto son:
- Dibuja el primer cono con los siguientes factores de escala: Sx=0.75 Sy=1.0 Sz=0.75.
- A continuación, dibuja dos nuevos conos aplicando los mismos factores de escala y trasladándolos sobre el eje Y, Tx=0.0 Ty=0.25 Tz= 0.0.
- Finalmente, dibuja el tronco llamando a la función igWireRulo(int pu, int pv).
Desde la función principal (main) debes llamar una única vez a CreaAbeto(). Para dibujar el abeto como una display list, llama desde la función Dibuja() a:
glCallList (abeto);
3. Construye el mismo abeto pero mediante el uso de las funciones glPushMatrix() y glPopMatrix(). Es decir, haz que cada primitiva tenga sus transformaciones propias y que estas no afecten a las otras primitivas. Declara una nueva display list (abetoPush) y crea la display list para dibujar el abeto con las funciones glPush() y glPop() y llámala CreaAbetoPush().Comprueba que los dos abetos son iguales dibujando uno sobre otro con distintos colores.
4. Utilizando las primitivas de la librería glig.c, construye una display list para una escalera de caracol (escalera). Introduce el código en la función CreaEscalera(). Los pasos son los siguientes:
- Dibuja una caja a modo de eje de la escalera de altura=2.0 y lado= 0.2
- Realiza un bucle para dibujar cada uno de los escalones. Los escalones están escalados con factores de escala, Sx=0.5 Sy= 0.05 Sz=0.1. La separación entre escalones es de 0.2.
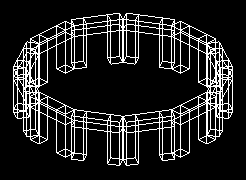
5. Realiza la construcción de la figura (lo más parecida posible) de acuerdo con los siguientes pasos:
- En primer lugar define una función Arco() que construya un arco individual (con tres cajas)
- Utiliza ese elemento para realizar la construcción circular.

 examinar.c
examinar.c
/*************************************************************************/
/* */
/* examinar.c */
/* Rev. 2.0 01/01/2002 AUTORES: O. Belmonte, M. Chover, J. Ribelles */
/* */
/*************************************************************************/
/***************** INCLUDES DE LAS LIBRERIAS NECESARIAS ******************/
#include <GL/glut.h>
#include <stdio.h>
#include <stdlib.h>
#include "examinar.h"
#include "glig.h"
/******************************************************************************************/
/* Establece el area visible y el tipo de proyeccion */
/* Parametros: int ancho --> Ancho del area visible */
/* int alto --> Alto del area visible */
/* Salida: Ninguna */
/******************************************************************************************/
void TamanyoVentana (GLsizei ancho, GLsizei alto)
{
/* Definicion del viewport */
glViewport(0, 0, ancho, alto);
/* Definicion de la vista */
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(-2.0, 2.0, -2.0*(GLfloat)alto/(GLfloat)ancho, 2.0*(GLdouble)alto/(GLfloat)ancho, -2.0, 2.0);
}
/******************************************************************************************/
/* Abre una ventana OpenGL */
/* Parametros: int numeroArgumentos --> El numero de argumentos en la llamada al programa */
/* char ** listaArgumentos --> Vector de cadenas con cada argumento */
/* Salida: Ninguna */
/******************************************************************************************/
void AbreVentana (int numeroArgumentos, char ** listaArgumentos)
{
glutInit(&numeroArgumentos, listaArgumentos);
glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize (VentanaAncho, VentanaAlto);
glutInitWindowPosition (VentanaX, VentanaY);
glutCreateWindow (listaArgumentos[0]);
glutDisplayFunc (Dibuja);
glutReshapeFunc (TamanyoVentana);
glClearColor (0.0f, 0.0f, 0.0f, 0.0f); /* Establece el color de borrado */
glClear (GL_COLOR_BUFFER_BIT); /* Borra el buffer de color */
glColor3f (1.0f, 1.0f, 1.0f); /* Establece el color de dibujo */
}
/******************************************************************************************/
/* Define las acciones tras una pulsacion del teclado */
/* Parametros: unsigned char key --> Codigo de la tecla pulsada */
/* int x --> Coordenada x del cursor en el momento de pulsar la tecla */
/* int y --> Coordenada y del cursor en el momento de pulsar la tecla */
/* Salida: Ninguna */
/******************************************************************************************/
void Teclado (unsigned char tecla, int x, int y)
{
switch (tecla)
{
case 27 : /* Codigo de la tecla de Escape */
exit(0);
break;
}
}
/******************************************************************************************/
/* Define las acciones tras una pulsacion del teclado ampliado */
/* Parametros: unsigned char key --> Codigo de la tecla pulsada */
/* int x --> Coordenada x del cursor en el momento de pulsar la tecla */
/* int y --> Coordenada y del cursor en el momento de pulsar la tecla */
/* Salida: Ninguna */
/******************************************************************************************/
void TecladoAmpliado (int tecla, int x, int y)
{
switch (tecla)
{
case GLUT_KEY_UP : /* Pulsacion cursor arriba del teclado ampliado */
beta = beta + 15.0;
if (beta > 360.0) beta = beta - 360.0;
break;
case GLUT_KEY_DOWN : /* Pulsacion cursor abajo del teclado ampliado */
beta = beta - 15.0;
if (beta < 0.0) beta = beta + 360.0;
break;
case GLUT_KEY_RIGHT : /* Pulsacion cursor derecha del teclado ampliado */
alfa = alfa + 15.0;
if (alfa > 360.0) alfa = alfa - 360.0;
break;
case GLUT_KEY_LEFT : /* Pulsacion cursor izquierda del teclado ampliado */
alfa = alfa - 15.0;
if (alfa < 0.0) alfa = alfa + 360.0;
break;
}
glutPostRedisplay ();
}
/* Rutina de definiciÛn de eventos */
/******************************************************************************************/
/* Inicia las funciones de callback */
/* Parametros: Ninguno */
/* Salida: Ninguna */
/******************************************************************************************/
void IniciaFuncionesCallback (void)
{
glutKeyboardFunc (Teclado);
glutSpecialFunc (TecladoAmpliado);
}
/******************************************************************************************/
/* Funcion de dibujado */
/* Parametros: Ninguno */
/* Salida: Ninguna */
/******************************************************************************************/
void Dibuja (void)
{
glClear (GL_COLOR_BUFFER_BIT);
/* Transformacion de la camara */
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glRotated (beta, 1.0,0.0,0.0);
glRotated (-alfa, 0.0,1.0,0.0);
glCallList (cuadrica);
glCallList(abetoPush);
glCallList (abeto);
glCallList(escalera);
glCallList(patio);
/* Objetos */
//glutWireTeapot(1.0);
//glutWireIcosahedron();
//glutWireTetrahedron();
//glutWireOctahedron();
//glutWireDodecahedron();
//glutWireTorus(0.2,0.9,18,20);
//glutWireCone(0.5, 2.0, 14, 14);
//glutWireCube(1.0);
//glutWireSphere(1, 20,50);
//igCreateQuadricObject(50,80,0,0,1.0, 1, 1);
//igWireSphere (50, 50);
//igWireRulo (200, 200);
//igWireDado (60, 60);
//igWireSemiSphere (50, 50); // s1 y s2 a 1, uMax= 1, vMax= 0.5 */
//igWireCubo();
glFlush();
}
void IniciaCuadricas (void)
{
cuadrica = glGenLists (1);
escalera=glGenLists(1);
abeto=glGenLists(1);
abetoPush=glGenLists(1);
patio=glGenLists(1);
if (cuadrica != 0) /* Cero no es un identificador valido para una display list */
{
//glNewList (cuadrica, GL_COMPILE);
//igCreateQuadricObject (20,20,0,0,1.0f, 1.0f, 1.0f);
//igWireCubo();
//igWireRulo(20, 20);
//igWireCone(10,3);
//igWireSphere(30, 30);
//glEndList ();
printf("Cuadratica\n");
}
if (escalera!=0)
{
//CreaEscalera();
printf("Escalera\n");
}
if (abeto!=0)
{
//CreaAbeto();
printf("Abeto\n");
}
if (abetoPush!=0)
{
glNewList(abetoPush, GL_COMPILE);
//CreaAbetoPush();
glEndList();
printf("AbetoPush\n");
}
if (patio!=0)
{
CreaPatio();
printf("patio\n");
}
}
/******************************************************************************************/
/* Funcion principal */
/* Parametros: int numeroArgumentos --> El numero de argumentos en la llamada al programa */
/* char ** listaArgumentos --> Vector de cadenas con cada argumento */
/* Salida: Un entero que se devuelve al sistema al acabar la ejecucion del programa */
/******************************************************************************************/
int main(int numArgumentos, char ** listaArgumentos)
{
/* CreaciÛn de la ventana de la aplicaciÛn */
AbreVentana (numArgumentos, listaArgumentos);
/* Rutinas para el control de eventos */
IniciaFuncionesCallback ();
IniciaCuadricas();
/* A la espera de eventos.... */
glutMainLoop();
return (0);
}
glig.c
/*************************************************************************/
/* */
/* glig.c LIBRERIA DE MODELADO GEOMETRICO */
/* */
/* Rev. 2.0 01/01/2002 AUTORES: O. Belmonte, M. Chover, J. Ribelles */
/* */
/*************************************************************************/
/***************** INCLUDES DE LAS LIBRERIAS NECESARIAS ******************/
#include <GL/glut.h>
#include <math.h>
#include <stdio.h>
#include "glig.h"
#define PI 3.1415926535897932
#define ALFA (0.5-v)*PI
#define BETA 2*PI*u
/************************* FUNCIONES BASICAS **********************************************/
/******************************************************************************************/
/* Devuelve la coordenada x de un punto en R3 a partir de un punto (u,v) */
/* de un espacio parametrico en R2 */
/* Parametros: float u --> Primera coordenada de un punto en R2 */
/* float v --> Segunda coordenada de un punto en R2 */
/* float R --> Radio de la esfera envolvente */
/* float s1 --> Numero de divisiones en u */
/* float s2 --> Numero de divisiones en v */
/* Salida: La coordenada x de un punto en R3 */
/******************************************************************************************/
float xSuperQuadric (float u, float v, float R, float s1, float s2)
{
float cosalfa, cosbeta, powcosalfa, powcosbeta;
cosalfa = (float)cos(ALFA);
cosbeta = (float)cos(BETA);
if(cosalfa > 0.0)
powcosalfa = (float)pow(cosalfa,s1);
else
powcosalfa =(float) - pow(- cosalfa,s1);
if(cosbeta > 0.0)
powcosbeta = (float)pow(cosbeta,s2);
else
powcosbeta = (float) - pow(- cosbeta,s2);
return (R*powcosalfa*powcosbeta);
}
/******************************************************************************************/
/* Devuelve la coordenada y de un punto en R3 a partir de un punto (u,v) */
/* de un espacio parametrico en R2 */
/* Parametros: float u --> Primera coordenada de un punto en R2 */
/* float v --> Segunda coordenada de un punto en R2 */
/* float R --> Radio de la esfera envolvente */
/* float s1 --> Numero de divisiones en u */
/* float s2 --> Numero de divisiones en v */
/* Salida: La coordenada y de un punto en R3 */
/******************************************************************************************/
float ySuperQuadric (float u, float v, float R, float s1, float s2)
{
float sinalfa, powsinalfa;
sinalfa = (float)sin(ALFA);
if(sinalfa > 0.0)
powsinalfa = (float)pow(sinalfa,s1);
else
powsinalfa = (float)- pow(- sinalfa,s1);
return (R*powsinalfa);
}
/******************************************************************************************/
/* Devuelve la coordenada de un punto en R3 a partir de un punto (u,v) */
/* de un espacio parametrico en R2 */
/* Parametros: float u --> Primera coordenada de un punto en R2 */
/* float v --> Segunda coordenada de un punto en R2 */
/* float R --> Radio de la esfera envolvente */
/* float s1 --> Numero de divisiones en u */
/* float s2 --> Numero de divisiones en v */
/* Salida: La coordenada z de un punto en R3 */
/******************************************************************************************/
float zSuperQuadric(float u, float v, float R, float s1, float s2)
{
float cosalfa, sinbeta, powcosalfa, powsinbeta;
cosalfa = (float)cos(ALFA);
sinbeta=(float)sin(BETA);
if(cosalfa > 0.0)
powcosalfa = (float)pow(cosalfa,s1);
else
powcosalfa=(float) - pow(- cosalfa,s1);
if(sinbeta > 0.0)
powsinbeta = (float)pow(sinbeta,s2);
else
powsinbeta = (float) - pow(- sinbeta,s2);
return(R*powcosalfa*powsinbeta);
}
/********************** RUTINA DE DIBUJO *********************************/
void igCreateQuadricObject (int pu, int pv, float uMax, float vMax, float R, float s1, float s2)
{
/* pu es el numero de divisiones en u */
/* pv es el numero de divisiones en v*/
float u, v;
float iniu,iniv;
float inc_u; //incremento de u
float inc_v; //incremento de v
float x, y, z; /*almanezaran las coordenadas en el espacio tridimensional*/
int i,j;/*contadores para los bucles for*/
v= uMax;
u =vMax;
iniu=u;
iniv=v;
/*El maximo valor de u y v es 1 y el minimo es 0 por lo tanto debemos de distribuir
las partes exigidas en la distancia establecida entre el valor de inicialización y
el maximo valor*/
inc_u= (1.0f-u)/pu;
inc_v= (1.0f-v)/pv;
//Dibujamos los paralelos de la esfera
//tantas circunfencias como partes de v
for (j=0;j<pv;j++)
{
glBegin (GL_LINE_LOOP);//Indicamos a openGL el modo de dibujado
//indicamos los puntos (partes de u) que formaran la circunferencia
for (i= 0; i<= pu; i++)
{
x= xSuperQuadric (u, v, R, s1, s2);//indicamos la coordenada x del punto
y= ySuperQuadric (u, v, R, s1, s2);//indicamos la coordenada y del punto
z= zSuperQuadric (u, v, R, s1, s2);//indicamos la coordenada z del punto
glVertex3f (x, y, z); //pintamos el punto en el espacio tridimensional
u= u+ inc_u;//avanzamos hasta el siguiente putno
//printf("valor de v=%f valor de u=%f\n",v,u);
if (u>1){u=iniu;}
}
glEnd();//indicamos a openGL que hemos acabado de indicar los puntos de la circunferencia
v+=inc_v;//avanzamos a la siguiente circunferencia paralela
}
u=iniu;
v=iniv;
//Dibujamos os meridianos de la esfera
//tantos meridianos como partes de v
for (j=0;j<pu;j++)
{
glBegin(GL_LINE_STRIP);//Indicamos a OpenGL el modo de dibujado
//Indicamos los puntos (partes de v) que formaran el meridiano
v=iniv;
for(i=0;i<=pv;i++)
{
x= xSuperQuadric (u, v, R, s1, s2);//indicamos la coordenada x del punto
y= ySuperQuadric (u, v, R, s1, s2);//indicamos la coordenada y del punto
z= zSuperQuadric (u, v, R, s1, s2);//indicamos la coordenada z del punto
glVertex3f (x, y, z); //pintamos el punto en el espacio tridimensional
v+=inc_v;//avanzamos hasta el siguiente punto
//printf("valor de v=%f valor de u=%f\n",v,u);
}
//printf("Meridiano dibujado\n\n");
glEnd();//Indicamos a openGL que ya hemos señalado los puntos del meridiano
u+=inc_u;//avanzamos al siguiente meridiano
}
}
void igWireSphere (int pu, int pv)
{
/* s1 y s2 a 1 */
igCreateQuadricObject(pu,pv,0,0,1.0, 1, 1);
}
void igWireRulo (int pu, int pv)
{
/* s1= 0.5, s2= 1 */
igCreateQuadricObject(pu,pv,0,0,1.0, 0.5, 1);
}
void igWireDado (int pu, int pv)
{
/* s1= 0.5, s2 =0.5 */
igCreateQuadricObject(pu,pv,0,0,1.0, 0.5, 0.5);
}
void igWireSemiSphere (int pu, int pv)
{
/* s1 y s2 a 1, uMax= 1, vMax= 0.5 */
igCreateQuadricObject(pu,pv,0,0.5,1.0, 1, 1);
}
void igWireCubo (void)
{
//Centramos en el origen de las coordenadas
//El radio es 1
glBegin (GL_LINE_LOOP);
//aristas traseras
glVertex3f(-0.5,-0.5,-0.5);
glVertex3f(0.5, -0.5, -0.5);
glVertex3f(0.5,0.5,-0.5);
glVertex3f(-0.5,0.5,-0.5);
glVertex3f(-0.5,-0.5,-0.5);
//parte delantera
glVertex3f(-0.5,-0.5,0.5);
glVertex3f(-0.5,0.5,0.5);
glVertex3f(0.5,0.5,0.5);
glVertex3f(0.5,-0.5,0.5);
glVertex3f(-0.5,-0.5,0.5);
//lado izquierdo
glVertex3f(-0.5,-0.5,-0.5);
glVertex3f(-0.5,-0.5,0.5);
glVertex3f(-0.5,0.5,0.5);
glVertex3f(-0.5,0.5,-0.5);
glVertex3f(0.5,0.5,-0.5);
glVertex3f(0.5,0.5,0.5);
glVertex3f(0.5,-0.5,0.5);
glVertex3f(0.5,-0.5,-0.5);
glEnd ();
}
void igWireCone (int pu, int pv)
{
/* s1= 2.0, s2= 1.0, uMax= 1.0, vMax= 0.5 */
igCreateQuadricObject(pu, pv, 0.5, 0, 1, 2.0, 1.0);
}
void CreaAbetoPush(void)
{
//abetoPush= glGenLists(1);
if (abetoPush != 0)
{
glNewList( abetoPush, GL_COMPILE);
glColor3f(1,0,0);
glPushMatrix();
glRotated(180,0,0,1);
glScalef(0.75, 1, 0.75);
igWireCone(20, 20);
glPopMatrix();
glPushMatrix();
glTranslatef(0,0.25, 0);
glRotated(180,0,0,1);
glScalef(0.75, 1, 0.75);
glScalef(0.75, 1, 0.75);
igWireCone(20, 20);
glPopMatrix();
glPushMatrix();
glTranslatef(0, 0.5, 0);
glRotated(180,0,0,1);
glScalef(0.75, 1, 0.75);
glScalef(0.75, 1, 0.75);
glScalef(0.75, 1, 0.75);
igWireCone(20, 20);
glPopMatrix();
glPushMatrix();
glRotated(180,0,0,1);
glScalef(0.75, 1, 0.75);
glScalef(0.75, 1, 0.75);
glScalef(0.75, 1, 0.75);
glScalef(0.5, 1, 0.5);
igWireRulo(15, 5);
glPopMatrix();
glEndList();
}
else
{
printf("Error al crear abetoPush\n");
}
}
void CreaAbeto (void)
{
//abeto = glGenLists (1);
if (abeto != 0) /* Cero no es un identificador valido para una display list */
{
glNewList (abeto, GL_COMPILE);
/* Código para dibujar el abeto */
/*Sx=0.75 Sy=1.0 Sz=0.75*/
glColor3f(0,1,0);
glRotated(180,0,0,1);
glScalef(0.75,1,0.75);
igWireCone(20, 20);
glScalef(0.75,1,0.75);
glTranslatef(0,-0.25,0);
igWireCone(20, 20);
glScalef(0.75,1,0.75);
glTranslatef(0,-0.25,0);
igWireCone(20, 20);
glTranslatef(0, 0.5, 0);
glScalef(0.5, 1, 0.5);
igWireRulo(15, 5);
glEndList ();
}
}
void CreaEscalera(void)
{
int x;
glNewList(escalera, GL_COMPILE);
printf("mierda\n");
//# Dibuja una caja a modo de eje de la escalera de altura=2.0 y lado= 0.2
escalon();
for(x=0;x<100;x++)
{
glPushMatrix();
glRotated(90,1,0,0);
//Sx=0.5 Sy= 0.05 Sz=0.1
glScalef(0.5, 0.5, 0.1);
glTranslatef(0, 0,-x*(0.2));
glRotated((360/50)*x,0,0,1);
escalon();
glPopMatrix();
}
glEndList();
}
void escalon(void)
{
glBegin (GL_LINE_LOOP);
//base
glVertex3f(-0.1,0,-0.1);
glVertex3f(0.1,0,-0.1);
glVertex3f(0.1,0,0.1);
glVertex3f(-0.1,0,0.1);
glVertex3f(-0.1,0,-0.1);
//subimos
glVertex3f(-0.1,2,-0.1);
glVertex3f(0.1,2,-0.1);
//bajamos y subimos
glVertex3f(0.1,0,-0.1);
glVertex3f(0.1,2,-0.1);
glVertex3f(0.1,2,0.1);
//bajamos y subimos
glVertex3f(0.1,0,0.1);
glVertex3f(0.1,2,0.1);
glVertex3f(-0.1,2,0.1);
//bajamos y subimos
glVertex3f(-0.1,0,0.1);
glVertex3f(-0.1,2,0.1);
glVertex3f(-0.1,2,-0.1);
glEnd();
}
void CreaPatio(void)
{
int x;
glNewList( patio , GL_COMPILE);
for(x=0;x<12;x++)
{
glPushMatrix();
glScalef(0.2, 0.2, 0.2);
glRotated(30*x, 0, 1, 0);
glTranslatef(0, 0, -4);
arco();
glPopMatrix();
}
glEndList();
}
void arco(void)
{
glPushMatrix();
//glColor3f(1, 0, 0);//rojo
glTranslatef(-0.75, 0, 0);
columna();
glPopMatrix();
glPushMatrix();
//glColor3f(0, 1, 0);//verde
glTranslatef(0.75, 0, 0);
columna();
glPopMatrix();
glPushMatrix();
//glColor3f(0, 0, 1);//azul
glRotated(270, 0, 0, 1);
glTranslatef(-1.75, -1, 0);
columna();
glPopMatrix();
}
void columna(void)
{
glBegin (GL_LINE_LOOP);
//base
glVertex3f(-0.25,0,-0.25);
glVertex3f(0.25,0,-0.25);
glVertex3f(0.25,0,0.25);
glVertex3f(-0.25,0,0.25);
glVertex3f(-0.25,0,-0.25);
//subimos
glVertex3f(-0.25,2,-0.25);
glVertex3f(0.25,2,-0.25);
//bajamos y subimos
glVertex3f(0.25,0,-0.25);
glVertex3f(0.25,2,-0.25);
glVertex3f(0.25,2,0.25);
//bajamos y subimos
glVertex3f(0.25,0,0.25);
glVertex3f(0.25,2,0.25);
glVertex3f(-0.25,2,0.25);
//bajamos y subimos
glVertex3f(-0.25,0,0.25);
glVertex3f(-0.25,2,0.25);
glVertex3f(-0.25,2,-0.25);
glEnd();
}
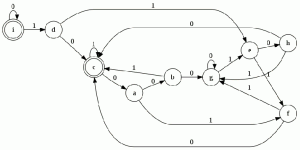
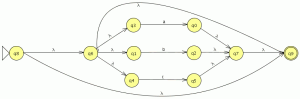
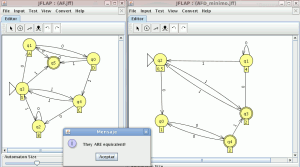
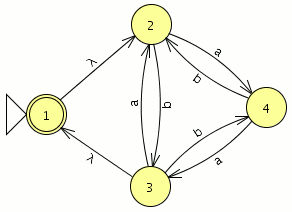
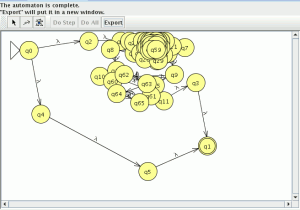
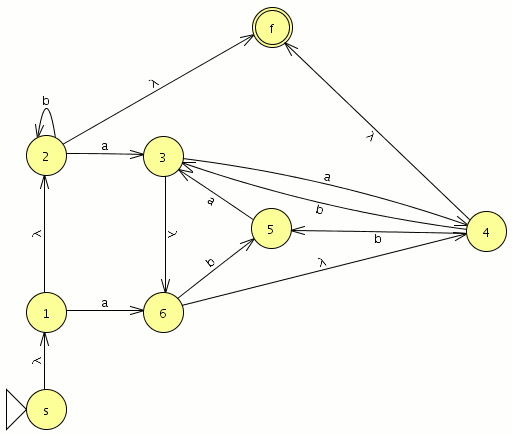
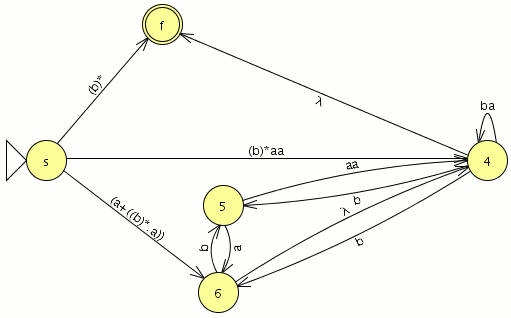
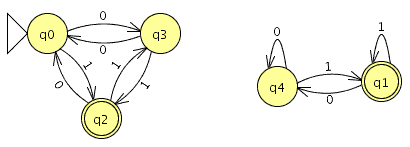
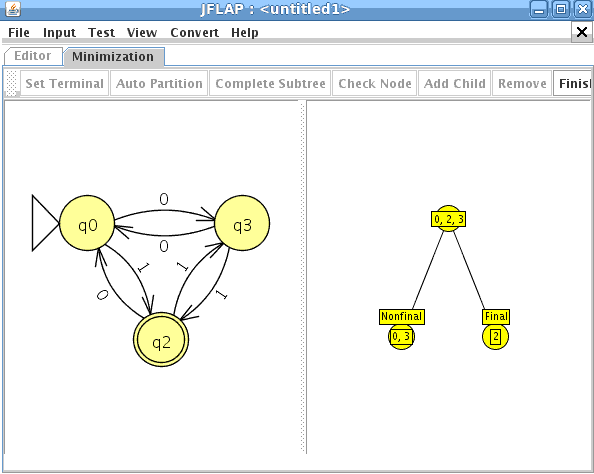
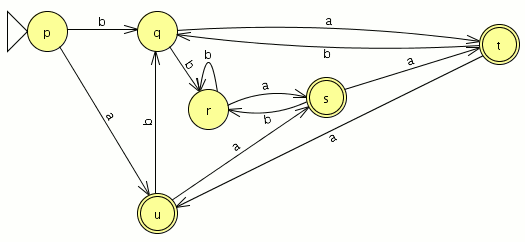
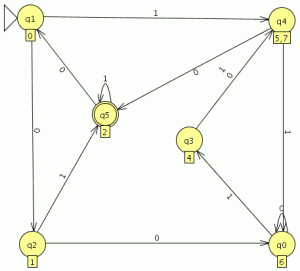 el numero de estados es el mismo el los dos autómatas y el lenguaje generado es equivalente por lo que debería de estar bien
el numero de estados es el mismo el los dos autómatas y el lenguaje generado es equivalente por lo que debería de estar bien
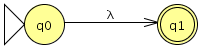

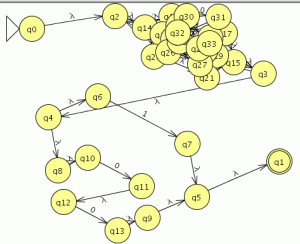
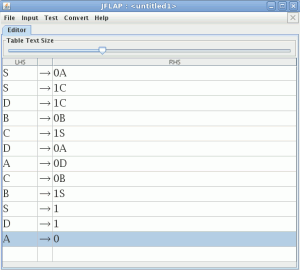
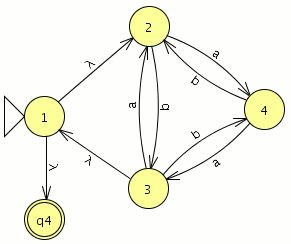
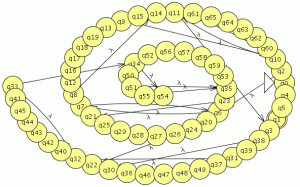
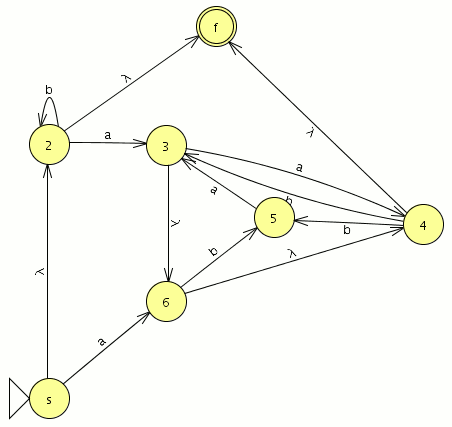
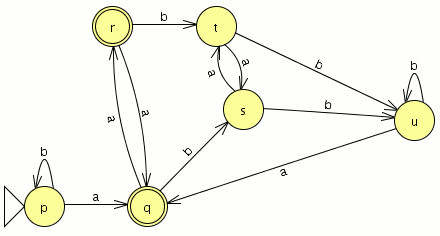
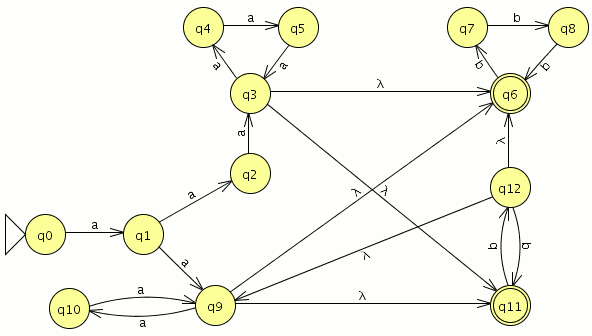
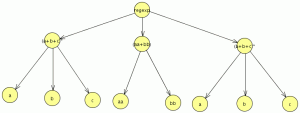 empezamos a modelar desde el segundo nivel ya que el primero es muy sencillo
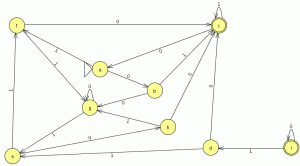
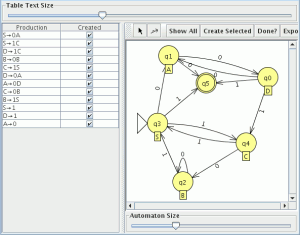
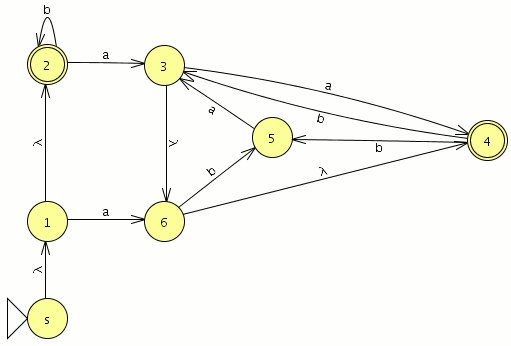
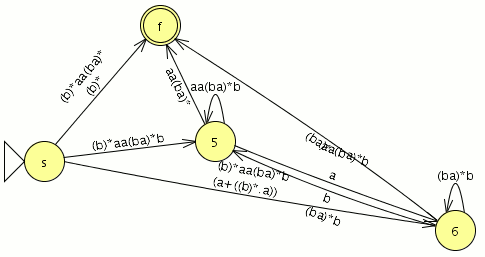
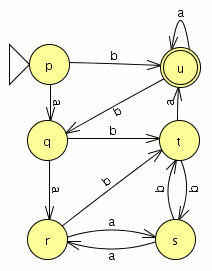
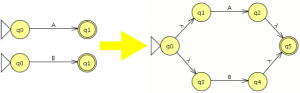
empezamos a modelar desde el segundo nivel ya que el primero es muy sencillo![]() comparamos con el JFlap y son equivalentes por lo tanto este paso va bien, ahora eliminamos las transiciones epsilon.
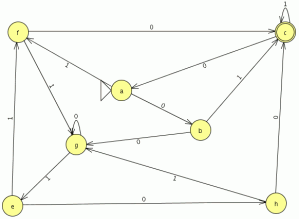
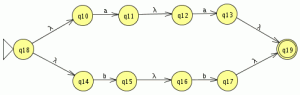
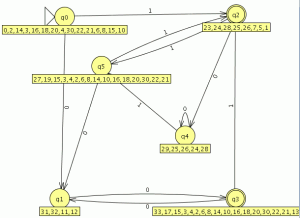
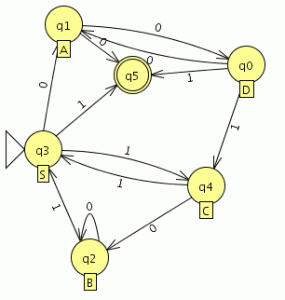
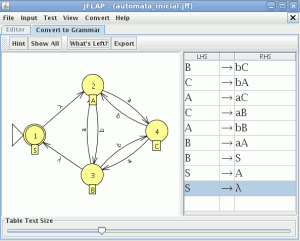
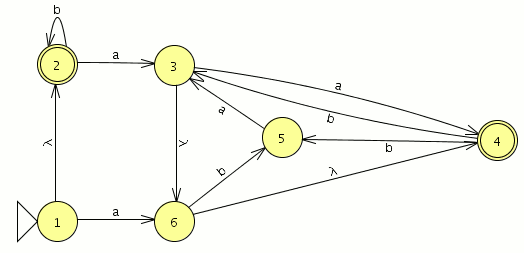
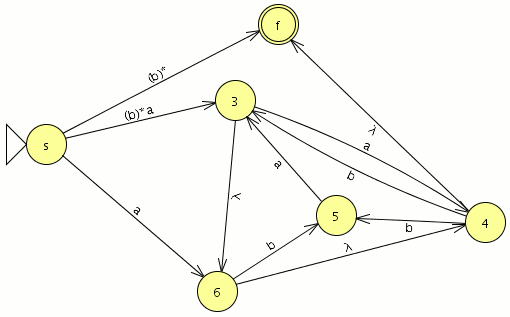
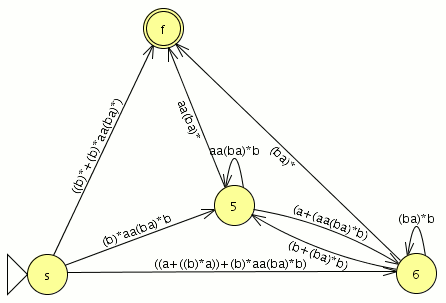
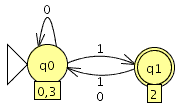
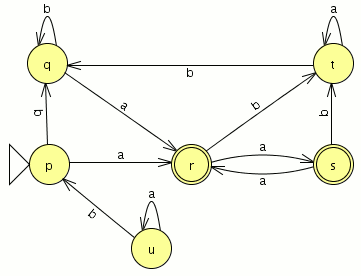
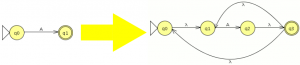
comparamos con el JFlap y son equivalentes por lo tanto este paso va bien, ahora eliminamos las transiciones epsilon.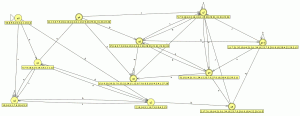 Y el AFD generado lo minimizamos
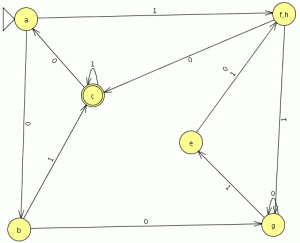
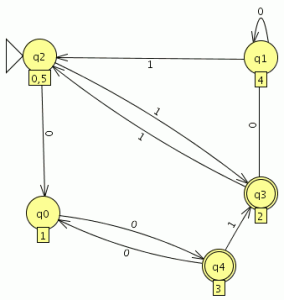
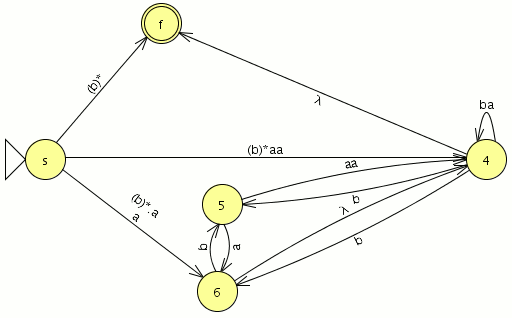
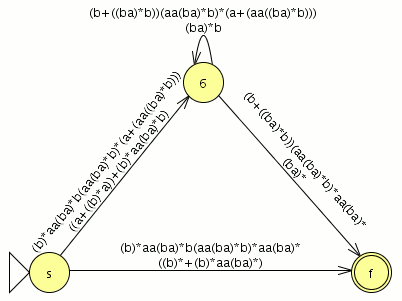
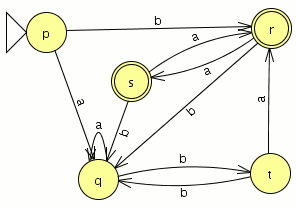
Y el AFD generado lo minimizamos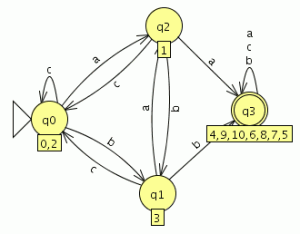 como es completo el indice(RL) es igual a 4 , si no fuera completo habría que añadir el estado de error siendo el indice(RL) igual al numero de estados del AFD mínimo + el estado de error
como es completo el indice(RL) es igual a 4 , si no fuera completo habría que añadir el estado de error siendo el indice(RL) igual al numero de estados del AFD mínimo + el estado de error