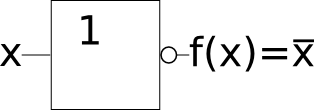
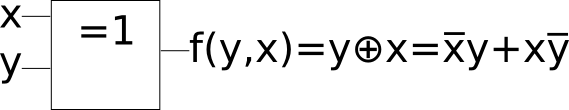Diseñar un circuito combinacional que compare la magnitud de dos números binarios A(a1 a0)2 y B(b1 b0)2. El circuito tendrá tressalidas C0, C1 y C2, que indicarán los tres resultados posibles, de acuerdo con la tabla de verdad siguiente.
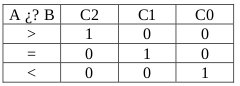
Para realizar ésta práctica sólo se dispone de los siguientes circuitos integrados:
- 1 integrado 74LS04 (NOT) 6 puertas
- 1 integrado 74LS08 (AND 2 entradas) 4 puertas
- 1 integrado 74LS11 (AND 3 entradas) 3 puertas
- 1 integrado 74LS32 (OR 2 entradas) 4 puertas
La salida de este circuito se visualizará en el display de 7 segmentos.
Tabla de Verdad
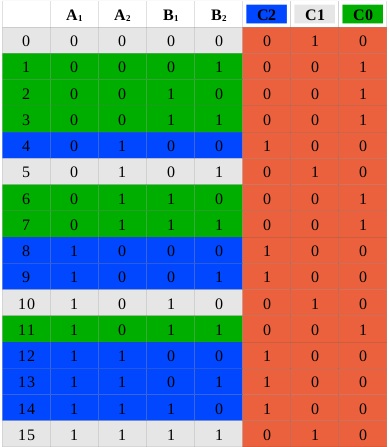
De aquí sacamos las siguientes formulas

Mapa de Karnaugh para C²
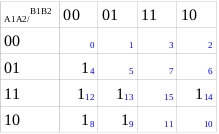
No podemos realizar grupos de1 elemento
Realizamos grupos de 2 elementos
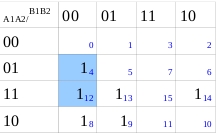
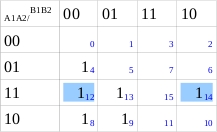
Realizamos Grupos de 4 elementos
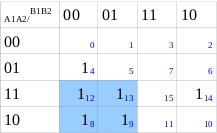
Grupo casillas 4,12 = A2 con 1, B1 y B2 con 0
Grupos casillas 14,12 = B2 con 0 A1,A2 con 1
Grupos Casillas 12,13,8,9 = B1 con 0 A1 con 1
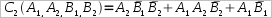
Mapa de Karnaugh para C¹
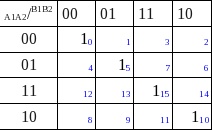
Agrupamos grupos de 2⁰ = 1
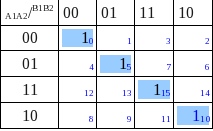
Agrupamos grupos de 2¹ = 2 no se puede hemos llegado al final
Grupo Casilla 0 A1,A2,B2,B1 con 0
Grupo Casilla 5 A1,B1 con 0 A2,B2 con 1
Grupo Casilla 15 A1,A2,B1,B2 con 1
Grupo Casilla 10 A1,B1 con 1 A2,B2 con 0
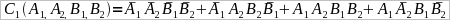
Mapa de Karnaugh para C⁰
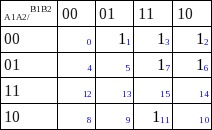
Agrupamos grupos de 2⁰ = 1

Agrupamos grupos de 2¹ = 2
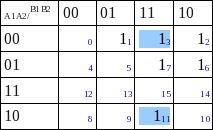
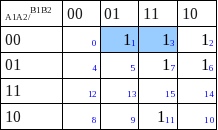
Agrupamos grupos de 2² = 4
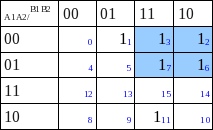
- Grupo Casillas 3,11 A2 con 0 B1,B2 con 1
- Grupo Casillas 3,1 A1,A2 con 0 B2 con 1

- Grupo Casillas 3,2,7,6 B1 con 1 A1 con 0
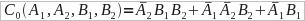
Asi que nuestro sistema digital queda definido por las siguientes operaciones
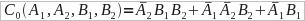
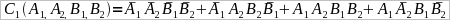
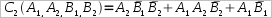
Truco del almendruco si Cx y Cy son =0 Cz = 1 (solo funciona cuando todo el mapa esta completo)
Como vamos algo cortos de material para montar el sistema eliminamos C1 16 multiplicaciones y 4 sumas
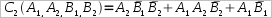
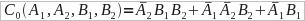
Si nos fijamos un poco no podemos montar C2 y C1 con los componentes diponibles, asi que vamos a buscarle los 3 pies al gato
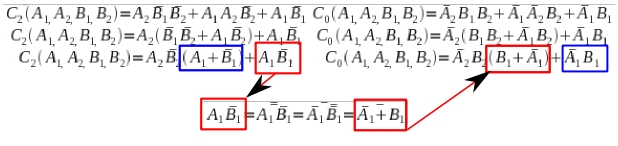
Ahora si que podemos montar el circuito en nuestro simulador preferido