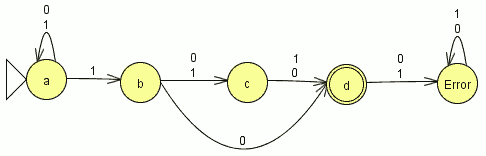
P1: Convierte el AFND de la hoja anterior en un autómata finito determinista. Incluye en tu solución la tabla de conversión tal como lo vimos en clase, la quintupla del AFD obtenido finalmente, y su grafo.
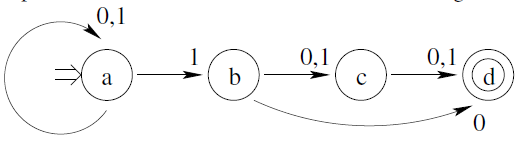
Partimos del siguiente AFND.
Añadimos el estado de Error.
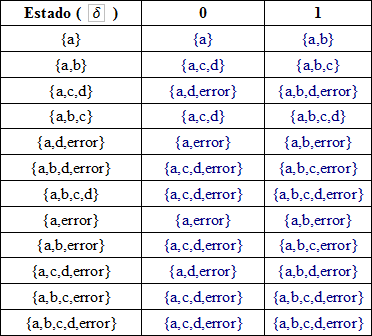
Comenzamos a crear la tabla de conversión
partimos del estado inicial {a}. con 0 vamos a {a} y con 1 a {a,b}
{a} ya pertenece al conjunto de estados, pero {a,b} no por lo tanto añadimos el estado {a,b}.
en el conjunto {a,b} con valor 0 a nos lleva a {a} y b nos lleva a {c,d} por lo tanto {a,b} con 0 nos lleva a {a,c,d} como {a,c,d} no esta en el conjunto de estados lo añadimos y añadimos las transiciones.
repetimos el procedimiento hasta que no se creen mas elementos para el conjunto de estados. quedándonos la siguiente tabla (a menos que me haya equivocado)
ahora pasamos la tabla a un grafo.
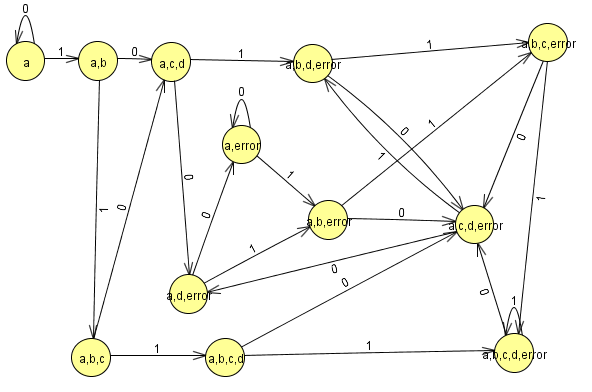Los primeros estados iniciales de nuestro AFND “con los que empezamos la tabla” son nuestros estados iniciales, en esta caso A.
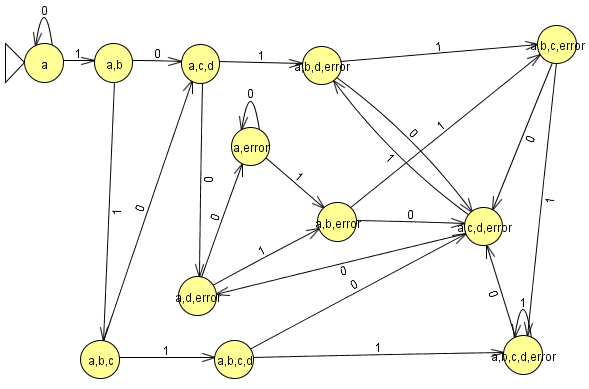Todo estado del AFD donde exista un estado final del AFND es final (en este caso todos donde este d)
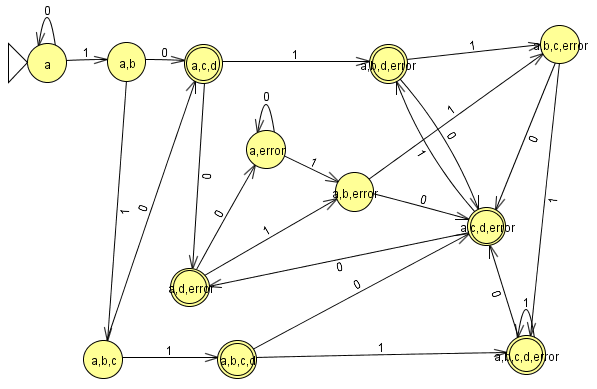Finalmente la quintupla queda definida por:
M=(∑,Q,δ,q0,F)
siendo
- ∑ El alfabeto
- Q Conjunto finito de estados
- δ la función de transición
- q0 conjunto de estados iniciales
- F conjunto de estados finales
- ∑ {0,1}
- Q [{a},{a,b},{a,c,d},{a,b,c},{a,d,error},{a,b,d,error},{a,b,c,d},{a,error},{a,b,error},{a,c,d,error},{a,b,c,error},{a,b,c,d,error}]
- δ es la tabla de transiciones
- q0 {a}
- F [{a,c,d},{a,d,error},{a,b,d,error},{a,b,c,d},{a,c,d,error},{a,b,c,d,error}]