Planificación de Proxectos Informaticos – La Fabulosa Vida de un IT

Código de Actividad
Tiempo Mínimo de Comienzo
Tiempo Máximo de Comienzo
Duración de la Actividad

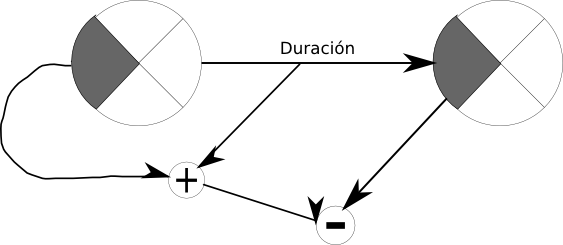
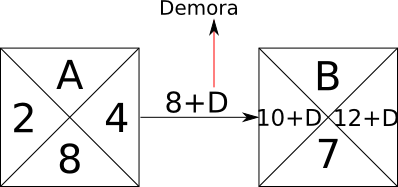
Relación Comienzo\Comienzo si D<8 (8=Duración de la actividad predecesora)

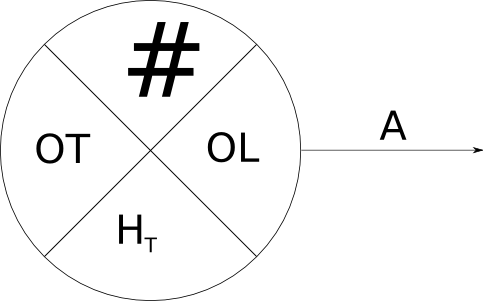
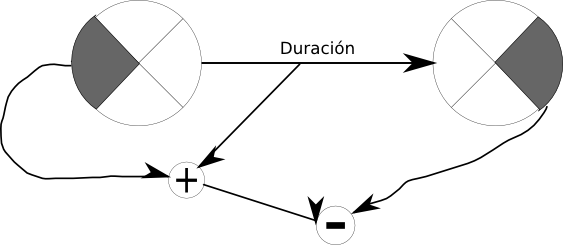
Tiempo Mínimo = es el mayor de las sumas de los tiempos mínimos anteriores mas el valor del arco.
Tiempo Máximo = elegir la menor (Porque es el tiempo maximo en el que puede acabar un actividad)

Holgura Total (Cuadrado) Diferencia entre los tiempos máximo y mínimo.

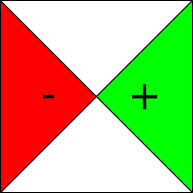Holgura Libre (Triangulo) El mínimo de (Tiempo mínimo de actividad siguiente – (Tiempo Mínimo de esa actividad+ Valor del Arco))

Nunca olvidar esto

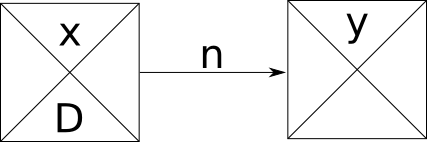Si n>=D -> Final Comienzo con demora = n-D
Si n<D ->Comienzo Comienzo con demora = n

Las Demoras de Roy
Si el valor del arco es mayor o igual que la duración de la actividad la relacion sera Final Comienzo con demora =n-D
Si el valor del arco es menor que la duración de la actividad la relación sera Comienzo Comienzo con demora = n

#	Numero de Identificación
OT	Ocurrencia mas temprana
OL	Ocurrencia mas tardía
H_L	Holgura Total
A	Actividad duración y holguras

Actividades Ficticias

Se usan Cuando hay mas de una actividad entre dos nodos

Tiempos Early Empezando por el primero sumas de tiempos early, en caso de varios caminos coger la mayor de las sumas
Tiempos Last Partiendo del ultimo se va restando del tiempo last la duración de las actividades en caso de varias coger la menor
Holguras

Siempre Holgura Total >= Holgura Libre

Holgura Total (Dentro del cuadrado)H.T = OL(n+1) – OT(n) – D

Holgura Libre (Dentro de un Triángulo)H.L = OT(n+1) – OT(n) – D

PERT solo admite relaciones Final \ Comienzo con Demora Nula

Tag: Planificación de Proxectos Informaticos

Metodo ROY

Diagramas de PERT