P1: Determina una expresión regular α que define el mismo lenguaje aceptado por el autómata de la Hoja 5, digamos M , es decir, se tiene que cumplir L(α) = L(M ). Documenta tu construcción suficientemente (tienes dos lados de una hoja).
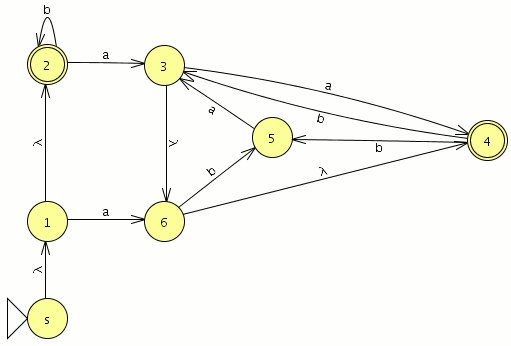
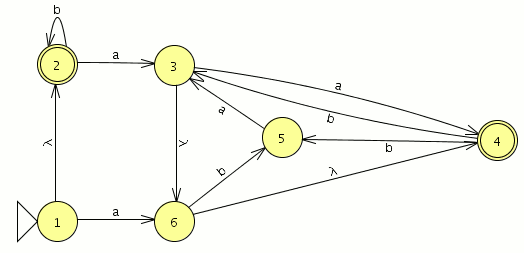
partimos del autómata de la hoja 5
para transformar nuestro AFND en una expresión regular necesitamos crear un AFNDG que este cumpla una serie de caracteristicas:
- El estado inicial no puede tener transiciones entrantes.
- El estado inicial debe de contar con transiciones salientes a los otros estados.
- Solo puede existir un estado final.
- El estado final no puede tener transiciones salientes.
- El estado final tiene que recibir transiciones entrantes de los otros.
- Excepto los estados inicial y final, cada estado tiene una única transición a los otros estados.
Transformando un AFND a un AFNDG
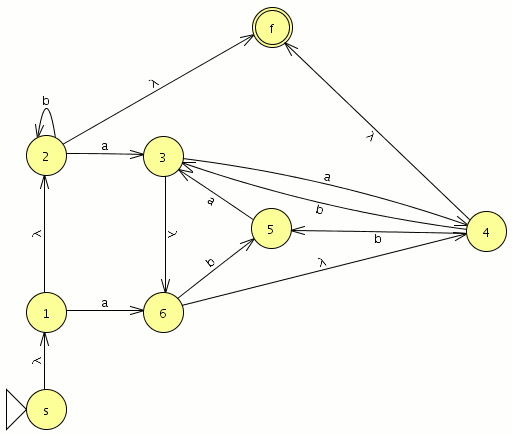
- Añadimos un nuevo estado inicial s con una transición epsilon al viejo estado inicial.
- Añadimos un nuevo estado final f con transiciones epsilon entrantes de los viejos estados finales.
- Si dos estados están conectados con múltiples transiciones, las reemplazamos por una única transición en la que su etiqueta es la unión de las etiquetas reemplazadas.
- Si dos estados no están conectados, añadimos una transición etiquetada con ∅ entre ellos (en ambas direcciones).
- Las transiciones ∅ nunca serán usadas.
Empezamos la transformación.
Paso 1:
Paso 2:
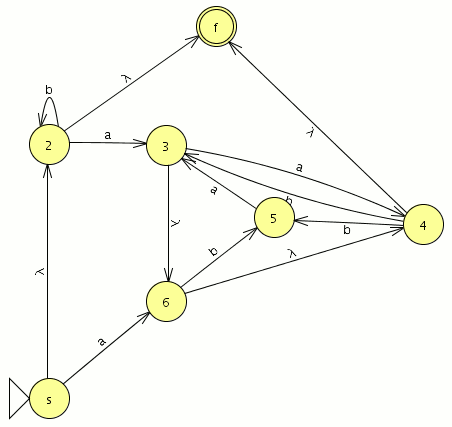
Paso 3:
No existen multiples transiciones que conecten 2 estados nuestro automata sigue como esta.
Paso 4:
Vamos a dejar las transiciones ∅ sin poner.
De AFNDG a Expresión Regular
Para convertir un AFNDG con k estados en una expresión regular:
- Si k=2, solo tenemos los estados f y s. La etiqueta de la transición de s a f es la expresión regular equivalente al AFNDG
- Si k>2 , entonces construimos un AFNDG con k-1 estados.
- a) Escogemos un estado distinto de s y f.
- b) Eliminamos el estado seleccionado del autómata
- c) Reconectamos las transiciones sueltas de forma apropiada.
- Para cada par de estados, qi y qj, cambiamos la etiqueta de la transición por una que pueda tomar el AFNDG desde qi a qj de forma directa o a través del estado que estamos seleccionado
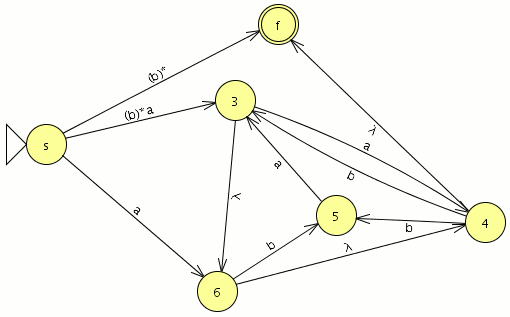
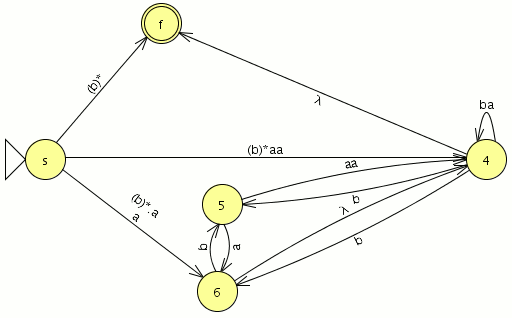
Comenzamos eliminando el estado marcado como 1
- no tiene transiciones consigo mismo
- las transiciones entrantes provienen del estado {s}
- las transiciones salientes se dirigen a los estados {2,6}
por lo tanto debemos crear los transiciones {s,2} y {s,6}
- la transición {s,2} es ε
- la transición {s,6} es a
las modelamos en el automata
no tenemos transiciones que tengan el mismo origen y destino continuamos
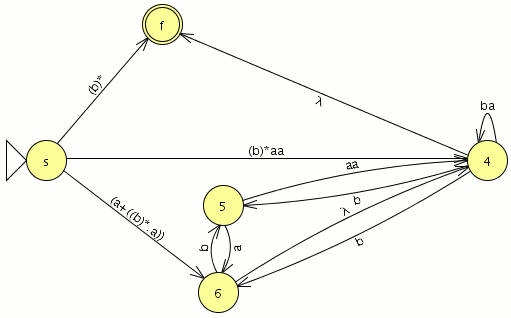
Eliminamos el estado marcado como 2:
- tiene transiciones consigo mismo.
- las transiciones entrantes provienen del conjunto de estados {s}
- las transiciones salientes se dirigen a los estados {3,f}
por lo tanto tenemos que generar las transiciones {s,3} y {s,f}, como hay transición consigo mismo debemos ingresar (b)* en el medio
- la transición {s,3} es (b)*.a
- la transición {s,f} es (b)*
tras la eliminación del estado 2 nuestro autómata toma la siguiente forma
no tenemos transiciones que tengan el mismo origen y destino continuamos
Eliminamos el estado marcado como 3
- no tiene transiciones consigo mismo
- las transiciones entrantes provienen de {s,4,5}
- las transiciones salientes se dirigen a {4,6}
por lo tanto debemos generar las transiciones {s,4},{s,6},{4,4},{4,6},{5,4},{5,6}
- la transición {s,4} genera (b)*.aa
- la transición {s,6} genera (b)*.a
- la transición {4,4} genera b.a
- la transición {4,6} genera b
- la transición {5,4} genera a.a
- la transición {5,6} genera a
tras la eliminación del estado 3 nuestro autómata toma la siguiente forma.
tenemos transiciones con mismo origen y destino, {s,6} las unimos y nuestro autómata toma la siguiente forma
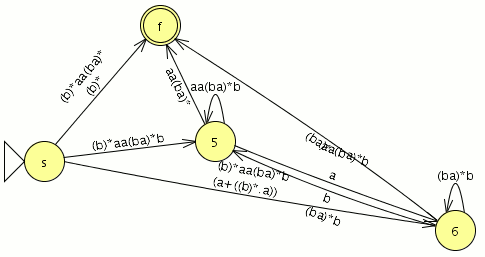
Eliminamos el estado marcado como 4
- tiene transiciones consigo mismo
- las transiciones entrantes provienen de {s,5,6}
- las transiciones salientes se dirigen a{5,6,f}
por lo tanto debemos generar las transiciones {s,5},{s,6},{s,f},{5,5},{5,6},{5,f},{6,5},{6,6},{6,f} como 4 tiene transición consigo mismo tenemos que insertar (ba)* en el medio
- la transición {s,5} genera (b)*aa(ba)*b
- la transición {s,6} genera (b)*aa(ba)*b
- la transición {s,f} genera (b)*aa(ba)*
- la transición {5,5} genera aa(ba)*b
- la transición {5,6} genera aa(ba)*b
- la transición {5,f} genera aa(ba)*
- la transición {6,5} genera (ba)*b
- la transición {6,6} genera (ba)*b
- la transición {6,f} genera (ba)*
tras la eliminación del estado 4 nuestro autómata toma la siguiente forma.
tenemos transiciones con el mismo origen y destino las unimos y nuestro autómata queda así
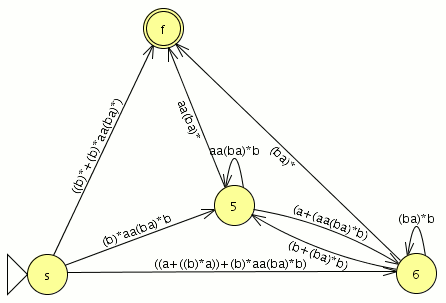
Eliminamos el estado marcado como 5
- tiene transiciones consigo mismo
- las transiciones entrantes provienen de {s,6}
- Las transiciones salientes se dirigen a {f,6}
las transiciones que debemos de crear son {s,f},{s,6},{6,f},{6,6} como tiene transiciones consigo mismo debemos insertar (aa(ba)*b)* en medio
- la transición {s,f} genera (b)*aa(ba)*b(aa(ba)*b)*aa(ba)*
- la transición {s,6} genera (b)*aa(ba)*b(aa(ba)*b)* (a+(aa((ba)*b)))
- la transición {6,f} genera (b+((ba)*b))(aa(ba)*b)*aa(ba)*
- la transición {6,6} genera (b+((ba)*b))(aa(ba)*b)*(a+(aa((ba)*b)))
tras la eliminación del estado 5 nuestro autómata toma la siguiente forma
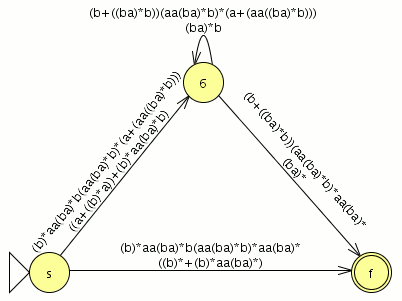tenemos transiciones con el mismo origen y destino así que las unimos
la transición {s,6} quedara ((b)*aa(ba)*b(aa(ba)*b)*(a+(aa((ba)*b)))+((a+((b)*a))+(b)*aa(ba)*b)) ==s6
la transición {s,f} quedara (((b)*aa(ba)*b(aa(ba)*b)*aa(ba)*)+((b)*+(b)*aa(ba)*)) == sf
la transicion {6,6} quedara (((b+((ba)*b))(aa(ba)*b)*(a+(aa((ba)*b))))+((ba)*b)) == 66
la transición {6,f} quedara (((b+((ba)*b))(aa(ba)*b)*aa(ba)*)+((ba)*)) == 6f
Eliminamos el estado marcado como 6
- tiene transiciones consigo mismo.
- las transiciones entrantes provienen de {s}
- las transiciones salientes se dirigen a {f}
por lo tanto deberemos de generar las transiciones {s,f} teniendo el cuenta como existe transición consigo mismo tenemos que insertar (66)* en medio
la transición {s,f} genera (sf)+((s6)(66)*(6f))
tras la eliminación del estado 6 nuestro autómata ya es la expresión regular.
((((b)*aa(ba)*b(aa(ba)*b)*aa(ba)*)+((b)*+(b)*aa(ba)*)))+((((b)*aa(ba)*b(aa(ba)*b)*(a+(aa((ba)*b)))+((a+((b)*a))+(b)*aa(ba)*b)))((((b+((ba)*b))(aa(ba)*b)*(a+(aa((ba)*b))))+((ba)*b)))*((((b+((ba)*b))(aa(ba)*b)*aa(ba)*)+((ba)*))))
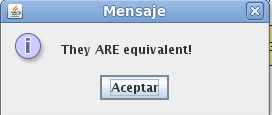
introducimos a expresión regular en JFlap la transformamos es un AFND y comparamos la equivalencia con el AFNDG y………………………
vamos que esta bien 🙂 a la 2ª fue la vencida
Fuentes:
http://vega.icu.ac.kr/~jiae/Automata_spring2008/DFA2RE.pdf